
����Ŀ������ע�س����̻�������������������½������ƻ�����ס����������繲800�꣬��������ÿ��12Ԫ����������ÿ��15Ԫ��������ϱ������ס�����������ijɻ��ʷֱ�Ϊ85%��90%��
��1�����������������繲��ȥ10500Ԫ����ס��������������������ꣿ
��2����Ҫʹ����������ܳɻ��ʲ�����88%��������������������ꣿ
��3���ڣ�2���������£�Ӧ���ѡ�����磬ʹ��������ķ�����ͣ��������ͷ��ã�
���𰸡�
��1���⣺�蹺���������x�꣬����������y�꣬������ã�
![]() ��
��
��� ![]() ��
��
�𣺹����������500�꣬��������300�꣮
��2���⣺��������繺��z�꣬������ã�
85%z+90%��800��z����800��88%��
���z��320��
�𣺼������������320�꣮
��3���⣺�蹺����������ķ���֮��Ϊm����
m=12z+15��800��z��=12000��3z��
�ڴ˺����У�m��z���������С
���Ե�z=320ʱ��mȡ����Сֵ������СֵΪ12000��3��320=11040Ԫ
�𣺹����������320�꣬��������480�꣬����������������ijɻ��ʲ�����88%����ʹ��������ķ�����ͣ�����ͷ���Ϊ11040Ԫ��
����������1���蹺���������x�꣬����������y�꣬�г������鼴�ɽ�����⣮��2�����ݼס�����������ijɻ�Ŀ�����800��88%���г�����ʽ���ɽ�����⣮��3���蹺����������ķ���֮��Ϊm����m=12z+15��800��z��=12000��3z������һ�κ��������ʼ��ɽ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Rt��ABC�У���BAC=90�㣬AB=AC=2����ACΪһ�ߣ��ڡ�ABC�ⲿ������ֱ��������ACD�����߶�BD�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
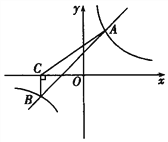
����Ŀ����ͼ��һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ����A��2��4����B��-4��
��ͼ����A��2��4����B��-4�� ![]() ������.
������.
��1���ֱ����һ�κ����뷴���������ı���ʽ��
��2������������������ֱ��д������ʽ![]() ��
��![]() �Ľ⼯��
�Ľ⼯��
��3������B��BC��x�ᣬ����ΪC������AC����S��ABC.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��DE����B=60�㣬AE��BC������Ϊ��E��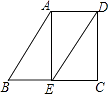
��1�����AED�Ķ�����
��2������EDC����ʲô����ʱ��AE��DC֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P�ӵ�A���������߶�AB�˶�����B��������ԭ·���أ���P���˶��������ٶȲ��䣬���Ե�BΪԲ�ģ��߶�BP��Ϊ�뾶��Բ�����S���P���˶�ʱ��t�ĺ���ͼ�����Ϊ�� ��
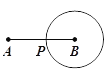
A. 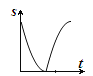 B.
B. 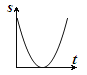 C.
C. 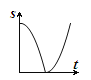 D.
D. 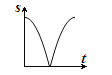
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
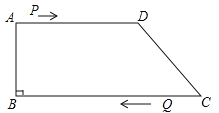
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����B=90�㣬AB=8cm��AD=12cm��BC=18cm����P�ӵ�A������2cm/s���ٶ���A��D��C�˶�����P�ӵ�A������ͬʱ��Q�ӵ�C��������1cm/s���ٶ����B�˶�������P�����Cʱ����QҲֹͣ�˶������P��Q�˶���ʱ��Ϊt�룮
��1�����˶���ʼ����tȡ��ֵʱ��PQ��CD��
��2�����˶���ʼ����tȡ��ֵʱ����PQCΪֱ�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
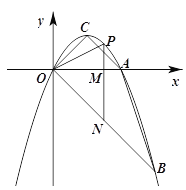
����Ŀ����ͼ��������y��ax2��bx����A��2��0����B��3����3�����㣬�����ߵĶ���ΪC������P��ֱ��OB�Ϸ����������ϣ�����P��ֱ��PM��y�ᣬ��x����M����OB��N�����P�ĺ�����Ϊm��
��1���������ߵĽ���ʽ����C��������
��2������PONΪ����������ʱ����N������Ϊ ������PMO����COBʱ����P������Ϊ ����ֱ��д�������
��3��ֱ��PN�ܷ��ı���ABOC��Ϊ�����Ϊ1��2�������֣����ܣ������m��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ݣ�0��1��2��3��3��5��5��10����λ���ǣ� ��
A.2.5
B.3
C.3.5
D.5
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com