
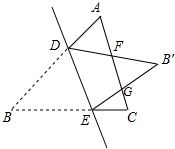
 已知△ABC中,AC=BC,点D、E分别在边AB、AC上,把△BDE沿直线DE翻折,使点B落在B′处,DB′,EB′分别交AC于点F、G,若∠ADF=80°,则∠EGC的大小为( )
已知△ABC中,AC=BC,点D、E分别在边AB、AC上,把△BDE沿直线DE翻折,使点B落在B′处,DB′,EB′分别交AC于点F、G,若∠ADF=80°,则∠EGC的大小为( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:填空题
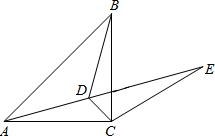 如图所示,已知点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA,则∠DCE的度数是105°.
如图所示,已知点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA,则∠DCE的度数是105°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
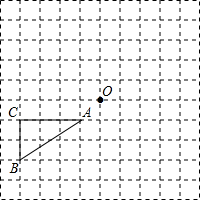 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有△ABC.点A、B、C、O均在小正方形的顶点上.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有△ABC.点A、B、C、O均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
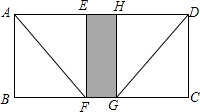 如图,将长方形纸片ABCD折叠,使得AB与AD重合,点B落在点E处,压平得折痕AF,则四边形ABFE是正方形:再将CD与AD重合,点C落在点H处,压平得折痕DG,则四边形CDHG也是正方形,展开后发现四边形EFGH正好与四边形ABCD相似,量得AB=10cm
如图,将长方形纸片ABCD折叠,使得AB与AD重合,点B落在点E处,压平得折痕AF,则四边形ABFE是正方形:再将CD与AD重合,点C落在点H处,压平得折痕DG,则四边形CDHG也是正方形,展开后发现四边形EFGH正好与四边形ABCD相似,量得AB=10cm查看答案和解析>>
科目:初中数学 来源: 题型:选择题
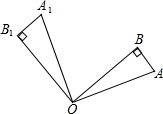 如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )| A. | 125° | B. | 65° | C. | 75° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=$\frac{3}{5}$,AB=4.
如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=$\frac{3}{5}$,AB=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com