
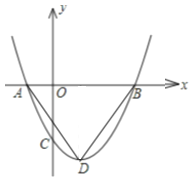
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D, 其图象与x轴的交点A、B的横坐标分别为﹣1,3.与y轴负半轴交于点C,当a=![]() 时,△ABD是_______三角形;要使△ACB为等腰三角形,则a值为______
时,△ABD是_______三角形;要使△ACB为等腰三角形,则a值为______
【答案】 等腰直角 ![]() 或
或![]()
【解析】解:如图1,∵二次函数y=ax2+bx+c(a>0)图象与x轴的交点A、B的横坐标分别为﹣1,3,a=![]() ,∴二次函数为y=
,∴二次函数为y=![]() (x+1)(x﹣3),整理得y=
(x+1)(x﹣3),整理得y=![]() x2﹣x﹣
x2﹣x﹣![]() ,∴y=
,∴y=![]() (x﹣1)2﹣2,∴顶点D(1,﹣2),作DE⊥AB于E,∴DE=2,DE垂直平分AB,∵AB=3+1=4,∴AE=DE=BE,∴∠DAB=∠ADE,∠ABD=∠BDE,∵AD=BD,∴∠DAB=∠DBA,∴∠DAB=∠ADE=∠ABD=∠BDE,∴∠ADB=∠DAB+∠CBA=90°,∴△ABD是等腰直角三角形;
(x﹣1)2﹣2,∴顶点D(1,﹣2),作DE⊥AB于E,∴DE=2,DE垂直平分AB,∵AB=3+1=4,∴AE=DE=BE,∴∠DAB=∠ADE,∠ABD=∠BDE,∵AD=BD,∴∠DAB=∠DBA,∴∠DAB=∠ADE=∠ABD=∠BDE,∴∠ADB=∠DAB+∠CBA=90°,∴△ABD是等腰直角三角形;
(2)要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,当AB=BC=4时,∵AO=1,△BOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣9=7,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣![]() ,与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=
,与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AB=AC=4时,∵AO=1,△AOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣1=15,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣![]() 与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AC=BC时
在△AOC中,AC2=1+c2,在△BOC中BC2=c2+9,∵AC=BC,∴1+c2=c2+9,此方程无解.
综上,要使△ACB为等腰三角形,则a值为![]() 或
或![]() ;
;
故答案为:等腰直角, ![]() 或
或![]() .
.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
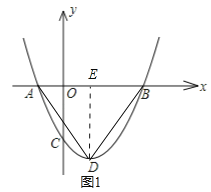
【题目】如图所示,∠AOB=90°,点C、D分别在射线OA、OB上,点E在∠AOB内部.
(1)根据语句画图形:
①画直线CE;
②画射线OE;
③画线段DE,
(2)结合图形,完成下面的填空:
①与∠ODE互补的角是 ;
②若∠BOE =![]() ∠AOE,则∠BOE的大小是 .
∠AOE,则∠BOE的大小是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
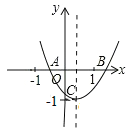
【题目】已知:二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①![]() =-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.
=-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
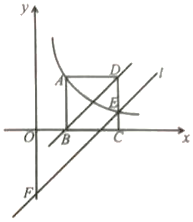
【题目】如图,正方形ABCD的顶点B、C在x轴的正半轴上,反个比例函数y= ![]() (k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n, ![]() ),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
A. (0,- ![]() )B. (0,-
)B. (0,- ![]() )
)
C. (0,-3)D. (0,- ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形ABCD的边AB在y轴正半轴上,顶点A的坐标为(0,2),设顶点C的坐标为(a,b).
(1)顶点B的坐标为 ,顶点D的坐标为 (用a或b表示);
(2)如果将一个点的横坐标作为x的值,纵坐标作为y的值,代入方程2x+3y=12成立,就说这个点的坐标是方程2x+3y=12的解.已知顶点B和D的坐标都是方程2x+3y=12的解,求a,b的值;
(3)在(2)的条件下,平移长方形ABCD,使点B移动到点D,得到新的长方形EDFG,
①这次平移可以看成是先将长方形ABCD向右平移 个单位长度,再向下平移 个单位长度的两次平移;
②若点P(m,n)是对角线BD上的一点,且点P的坐标是方程2x+3y=12的解,试说明平移后点P的对应点P′的坐标也是方程2x+3y=12的解.

查看答案和解析>>
科目:初中数学 来源: 题型:
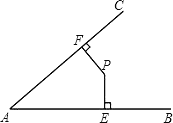
【题目】如图所示,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:
(1)PE=PF;
(2)点P在∠BAC的平分线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在13×7的网格中,每个小正方形边长都是1,其顶点叫做格点,如图A、B、D、E、M、P均为格点.
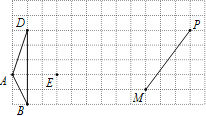
(1)请在网格中画□ABCD,要求C点在格点上.
(2)在(1)中□ABCD右侧画格点△EFG,并使EF=5,FG=3,EG=![]() .
.
(3)以MP为对角线画矩形MNPQ(M、N、P、Q按逆时针方向排列),使矩形MNPQ的面积为10.
(4)在直线AE上有一点W,使WB+WM的值最小,则这个最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个暗箱中装有红、黄、白三种颜色的乒乓球(除颜色外其余均相同).其中白球、黄球各1个,若从中任意摸出一个球是白球的概率是![]() .
.
(1)求暗箱中红球的个数;
(2)先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,求两次摸到的球颜色不同的概率(用树形图或列表法求解).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com