
【题目】(14分)如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
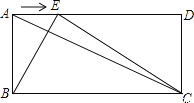
(1)若a=5,AC=13,求b.
(2)若a=5,b=10,当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
【答案】(1)b = 12 ;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)在矩形ABCD中,得到∠ABC=90°,利用勾股定理即可计算出结果.
(2)由∵BE⊥AC得到∠2+∠3=90°,由于∠1+∠3=90°,等量代换得到∠1=∠2,推出![]() 得到比例式,即可得到结论;
得到比例式,即可得到结论;
(3)点![]() 在线段
在线段![]() 上的任一点,且不与
上的任一点,且不与![]() 重合,当
重合,当![]() 与
与![]() 相似时,则
相似时,则![]() 当
当![]() (如图2),
(如图2),![]() 又
又![]() 由平行线的性质得到
由平行线的性质得到![]() 推出
推出![]() 得到比例式,进而可得得到一元二次方程
得到比例式,进而可得得到一元二次方程![]() 根据方程根的情况,得到结论.
根据方程根的情况,得到结论.
试题解析:(1)∵四边形ABCD是矩形,
![]()
∵AB=a=5, AC=13,
![]()
∴b=12;
![]() 如图1,∵BE⊥AC
如图1,∵BE⊥AC
![]()
又![]()
∴∠1 = ∠2,

又![]()
∴△AEB ∽△BAC,
∴![]() 即
即![]() ,
,
∴![]() .
.
(3)∵点E在线段AD上的任一点,且不与A、D重合,
∴当△ABE与△BCE相似时,则![]()
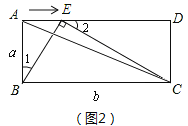
所以当△BAE ∽△CEB(如图2)
则∠1 = ∠BCE,
又BC∥AD,
∴∠2 = ∠BCE,
∴∠1 = ∠2 ,
又![]()
∴△BAE ∽△EDC,
∴![]() 即
即![]() ,
,
∴![]() ,
,
即![]() ,
,
当![]() ,
,
∵a>0,b>0, ∴![]()
即 ![]() 时,
时, ![]() .
.
综上所述:当a、b满足条件b = 2a时△BAE ∽△CEB,此时![]() (或x = a);
(或x = a);
当a、b满足条件b>2a时△BAE ∽△CEB,此时![]() .
.


科目:初中数学 来源: 题型:
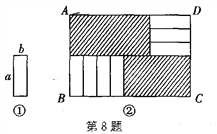
【题目】将7张如图①所示的长为a、宽为b(a>b)的小长方形纸片,按如图②所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设左上角与右下角的阴影部分的面积之差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a、b应满足( )
A. a=![]() b B. a=3b C. a=
b B. a=3b C. a=![]() b D. a=4b
b D. a=4b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.在同一平面内,两条直线的位置只有平行和垂直两种
B.两直线平行,同旁内角相等
C.过一点有且只有一条直线与已知直线平行
D.平行于同一条直线的两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在“助残日”举行了一次“手拉手、献爱心”的捐款活动,学校对已捐款学生人数及捐款金额情况进行了调查.图①表示的是各年级捐款人数占总捐款人数的百分比;图②是学校对学生的捐款金额情况进行抽样调查并根据所得数据绘制的统计图

(1)学校对多少名学生的捐款金额情况进行了抽样调查?
(2)这组捐款金额数据的平均数、中位数各是多少?
(3)若该校九年级共有400名学生捐款,估计全校学生捐款总金额大约多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下表回答问题:
x | 16 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 175.56 | 278.89 | 282.24 |
(1)272.25的平方根是
(2)![]() = ,
= , ![]() = ,
= , ![]() =
=
(3)设![]() 的整数部分为a,求﹣4a的立方根.
的整数部分为a,求﹣4a的立方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图所示,已知∠1 = ∠2,∠B = ∠C,可推得AB∥CD,

理由如下:
∵∠1 = ∠2(已知),且∠1 = ∠4(_____________________),
∴∠2 = ∠4(等量代换).
∴CE∥BF(__________________________).
∴∠_____= ∠3(________________________)
又∵∠B = ∠C(已知),
∴∠3= ∠B(等量代换),
∴AB∥CD(_____________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按HUI图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2018个点的坐标为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com