练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，D是Rt△ABC中斜边BC上的一点，且BD=AB，过D作BC的垂线，交AC于点E，若AE=5cm，DC=12 cm，则CE的长为_____________ cm.

    【答案】13

    【解析】根据已知条件，先证明△DBE≌△ABE，再根据全等三角形的性质（全等三角形的对应边相等）来求DE的长度．

    解：连接BE．


    ∵D为Rt△ABC中斜边BC上的一点，且BD=AB，过D作BC的垂线，交AC于E，
    ∴∠A=∠BDE=90°，
    ∴在Rt△DBE和Rt△ABE中，
    BD=AB（已知），BE=EB（公共边），
    ∴Rt△DBE≌Rt△ABE（HL），
    ∴AE=ED，
    又∵AE=5cm，
    ∴ED=5cm，

    CE=．
    故答案为：13．

    “点睛”本题主要考查了直角三角形全等的判定（HL）以及全等三角形的性质（全等三角形的对应边相等）．连接BE利用勾股定理是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】平面直角坐标系中，已知ABCD的三个顶点坐标分别是A（m，n），B（2，﹣1），C（﹣m，﹣n），则点D的坐标是（ ）
    A.（﹣2，1）
    B.（﹣2，﹣1）
    C.（﹣1，﹣2）
    D.（﹣1，2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】因式分解：

    （1）m3n﹣mn

    （2）ax2﹣4ax+4a

    查看答案和解析>>

    科目：初中数学 来源： 题型：

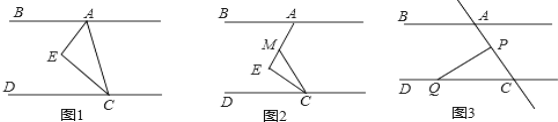
    【题目】如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°

    （1）请判断AB与CD的位置关系并说明理由；

    （2）如图2，当∠E=90°保持不变，移动直角顶点E，使∠MCE=∠ECD，当直角顶点E点移动时，问∠BAE与∠MCD是否存在确定的数量关系？并说明理由；

    （3）如图3，P为线段AC上一定点，点Q为直线CD上一动点，①当点Q在射线CD上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？猜想结论并说明理由．②当点Q在射线CD的反向延长线上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？直接写出猜想结论，不需说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y＝ax2+bx+c的顶点坐标是（﹣1，3），与x轴的交点是（2，0），则另一个交点为（　　）

    A. （0，﹣3） B. （﹣3，0） C. （﹣4，0） D. （﹣2，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一台电视机原价是2500元，现按原价的8折出售，则购买a台这样的电视机需要元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点，抛物线过A、B两点，且与x轴交于另一点C．

    （1）求b、c的值；

    （2）如图1，点D为AC的中点，点E在线段BD上，且BE=2ED，连接CE并延长交抛物线于点M，求点M的坐标；

    （3）将直线AB绕点A按逆时针方向旋转15°后交y轴于点G，连接CG，如图2，P为△ACG内以点，连接PA、PC、PG，分别以AP、AG为边，在他们的左侧作等边△APR，等边△AGQ，连接QR

    ①求证：PG=RQ；

    ②求PA+PC+PG的最小值，并求出当PA+PC+PG取得最小值时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，直线l1 经过A，B两点，直线l2的表达式为，且与x轴交于点D，两直线相交于点C.

    （1）求直线l1的表达式；

    （2）求△ADC的面积；

    （3）在直线l1上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】圆柱的侧面展开图是形．

    查看答案和解析>>

    同步练习册答案