
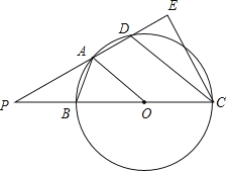
【题目】 如图,四边形ABCD内接于以BC为直径的圆,圆心为O,且AB=AD,延长CB、DA交于P,过C点作PD的垂线交PD的延长线于E,且PB=BO,连接OA.
(1)求证:OA∥CD;
(2)求线段BC:DC的值;
(3)若CD=18,求DE的长.
【答案】(1)详见解析;(2)![]() ;(3)DE=
;(3)DE=![]() .
.
【解析】
(1)连接BD,由圆周角定理可知∠BDC=90°,即CD⊥BD,再由AB=AD可知![]() ,则OA⊥BD,由此即可得出结论;
,则OA⊥BD,由此即可得出结论;
(2)设⊙O的半径为r,则PB=OB=OC=OA=r,再由OA∥CD可知,△OAP∽△CDP,故可得出![]() =
=![]() ,故可用r表示出CD的长,再求出BC:DC的值即可;
,故可用r表示出CD的长,再求出BC:DC的值即可;
(3)由OF∥CD,OB=OC根据中位线定理可以求出OF,AF;再根据勾股定理在Rt△DBC中可以求出BD,DF;接着在Rt△ADF中求出AD;然后利用平行线的性质得∠FAD=∠CDE证明△AFD∽△DEC,利用相似三角形的对应边成比例可以求出DE.
(1)证明:连接BD,交OA于点F.

∵BC是⊙O的直径,
∴∠BDC=90°,即CD⊥BD,
∵AB=AD,
∴![]()
∴OA⊥BD,
∴OA∥CD;
(2)解:设⊙O的半径为r,
∵PB=OB,
∴PB=OB=OC=OA=r,
∵OA∥CD,
∴△OAP∽△CDP,
∴![]() =
=![]() ,
,![]() =
=![]() ,解得CD=
,解得CD=![]() ,
,
∴![]() =
=![]() =
=![]() ;
;
(3)解:∵CD=18, CD=![]() ,∴r=12
,∴r=12
∵OF∥CD,![]() =
=![]() =
=![]() ,
,
∴OF=9,AF=3;
∵BD=![]() =6
=6![]() ,
,
∴DF=![]() BD=3
BD=3![]() ,
,
∴AD=![]() =6
=6![]() ;
;
∵∠AFD=∠DEC=90°,OA∥DC,∠FAD=∠CDE,
∴△AFD∽△DEC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ;
;
∴DE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(3,y2)是抛物线上两点,则y1<y2,其中说法正确的是( )
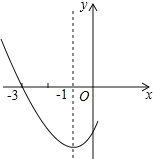
A.①②B.②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
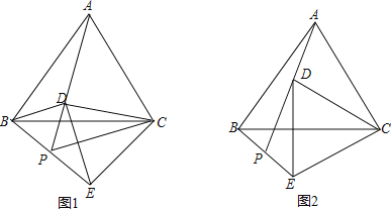
【题目】已知:△ABC是等边三角形,点D是△ABC(包含边界)平面内一点,连接CD,将线段CD绕C逆时针旋转60°得到线段CE,连接BE,DE,AD,并延长AD交BE于点P.
(1)观察填空:当点D在图1所示的位置时,填空:
①与△ACD全等的三角形是______.
②∠APB的度数为______.
(2)猜想证明:在图1中,猜想线段PD,PE,PC之间有什么数量关系?并证明你的猜想.
(3)拓展应用:如图2,当△ABC边长为4,AD=2时,请直接写出线段CE的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
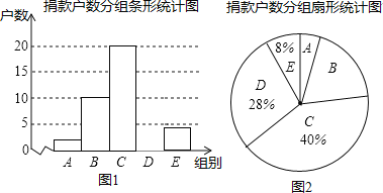
【题目】某社区组织“献爱心”捐款活动,并对部分捐款户数进行调查和分组统计,数据整理成如下统计图表(图中信息不完整).
捐款户数分组统计表
组别 | 捐款额(x)元 | 户数 |
A | 1≤x<100 | 2 |
B | 100≤x<200 | 10 |
C | 200≤x<300 | c |
D | 300≤x<400 | d |
E | x≥400 | e |
请结合以上信息解答下列问题:
(1)本次调查的样本容量是______;
(2)d=______,并补全图1;
(3)图2中,“B”所对应扇形的圆心角为______度;
(4)若该社区有500户住户,根据以上信息估计全社区捐款不少于300元的户数是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在矩形ABCD中,点N为边BC上不与B、C重合的一个动点,过点N作MN⊥BC交AD于点M,交BD于点E,以MN为对称轴折叠矩形ABNM,点A、B的对应点分别是G、F,连接EF、DF,若AB=6,BC=8,当△DEF为直角三角形时,CN的长为______.
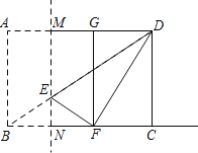
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
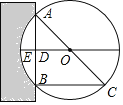
A. 13寸 B. 20寸 C. 26寸 D. 28寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax2﹣4ax+2a(a≠0)
(1)求抛物线的对称轴;
(2)若抛物线经过点A(m,y1),B(n,y2),其中﹣4<m≤﹣3,2<n≤3,请依据a的取值情况直接写出y1与y2的大小关系;
(3)若矩形CDEF的顶点分别为C(1,2),D(1,﹣4),E(5,﹣4),F(5,2),若该抛物线与矩形的边有且只有两个公共点(包括矩形的顶点),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ACB中,∠C=90°,BC=3cm,AC=3![]() cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为
cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为![]() cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
(1)如图①,连接PC,当t为何值时△APC∽△ACB,并说明理由;
(2)如图②,当点P,Q运动时,是否存在某一时刻t,使得点P在线段QC的垂直平分线上,请说明理由;
(3)如图③,当点P,Q运动时,线段BC上是否存在一点G,使得四边形PQGB为菱形?若存在,试求出BG长;若不存在请说明理由.
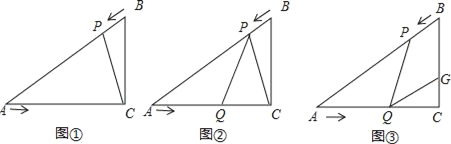
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com