
如图,在Rt△ABC中,∠C=90°,以BC为直径作⊙O交AB于点D,取AC的中点E,连结DE、OE.
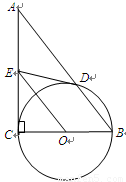
(1)求证:DE是⊙O的切线;
(2)如果⊙O的半径是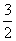 cm,ED=2cm,求AB的长.
cm,ED=2cm,求AB的长.
(1)证明△OCE≌△ODE. ∠OCE=∠ODE.又∠C=90°,故∠ODE =90°即可
(2)证明EO为中位线,则AB=2OE即可。
【解析】
试题分析:证明:(1)连结OD.
由O、E分别是BC、AC中点得OE∥AB.
∴∠1=∠2,∠B=∠3,又OB=OD.
∴∠2=∠3.
而OD=OC,OE=OE
∴△OCE≌△ODE.
∴∠OCE=∠ODE.
又∠C=90°,故∠ODE =90°.
∴DE是⊙O的切线.
(2)在Rt△ODE中,由 ,DE=2 得
,DE=2 得
又∵O、E分别是CB、CA的中点
∴AB=2·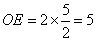
∴所求AB的长是5cm.
考点:圆的切线与中位线定理等
点评:本题难度中等,主要考查学生对圆和三角形问题的综合运用于掌握。为中考常见题型,要多加巩固训练,牢固掌握。


科目:初中数学 来源: 题型:
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
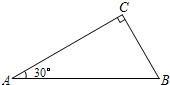 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
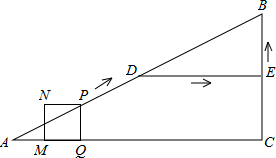 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com