
【题目】如图,在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.
(1)如图,若BC=BD,求证:CD=DE;
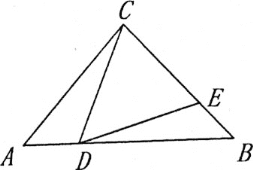
(2)如图,过点C作CH⊥DE,垂足为H,若CD=BD,![]() ,直接写出CE-BE的值为________.
,直接写出CE-BE的值为________.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先根据条件得出∠ACD=∠BDE,BD=AC,再根据ASA判定△ADC≌△BED,即可得到CD=DE;
(2)先根据条件得出∠DCB=∠CDE,进而得到CE=DE,再在DE上取点F,使得FD=BE,进而判定△CDF≌△DBE(SAS),得出CF=DE=CE,再根据CH⊥EF,运用三线合一即可得到FH=HE,最后得出DE-BE=DE-DF=EF=2HE=2.
(1)∵AC=BC,∠CDE=∠A,
∴∠A=∠B=∠CDE,
∠BDC=∠A+∠ACD
∴∠ACD=∠BDE,
又∵BC=BD,
∴BD=AC,
在△ADC和△BED中,
∴△ADC≌△BED(ASA),
∴CD=DE;
(2)![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,直线![]() 与两坐标轴交于
与两坐标轴交于![]() 、
、![]() 两点,点
两点,点![]() 为坐标原点,若在该坐标平面内有以点
为坐标原点,若在该坐标平面内有以点![]() (不与点
(不与点![]() 、
、![]() 、
、![]() 重合)为顶点的直角三角形与
重合)为顶点的直角三角形与![]() 全等,且这个以点
全等,且这个以点![]() 为顶点的直角三角形与
为顶点的直角三角形与![]() 有一条公共边,则所有符合条件的
有一条公共边,则所有符合条件的![]() 点个数为( )
点个数为( )
A. 9个 B. 7个 C. 5个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的右侧作正方形ADEF,连接CF.
(1)观察猜想:如图(1),当点D在线段BC上时,
①BC与CF的位置关系是: ;
②BC、CD、CF之间的数量关系为: (将结论直接写在横线上)
(2)数学思考:如图(2),当点D在线段CB的延长线上时,上述①、②中的结论是否仍然成立?若成立,请给予证明,若不成立,请你写出正确结论再给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAD=∠DAC,DF上AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.当t=________秒时,△DFE与△DMG全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.
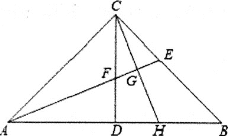
(1)直接写出∠CFE的度数________;
(2)求证:CF=BH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,∠BAC=90°.
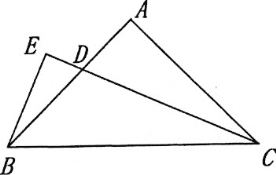
(1)如图,若CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,试探究线段BE和CD的数量关系,并证明你的结论
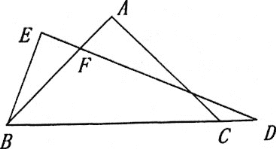
(2)如图,若点D在线段BC延长上,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE和FD的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
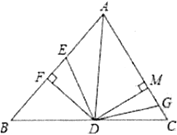
【题目】如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )
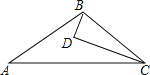
A. 1 B. 1.5 C. 2.5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
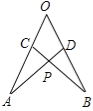
【题目】如图:在∠AOB的两边截取OA=OB,OC=OD,连接AD,BC交于点P,则下列结论中①△AOD≌△BOC,②△APC≌△BPD,③点P在∠AOB的平分线上。 正确的是 (填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com