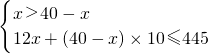某班“爱心社”的同学们计划在“5•12”汶川地震一周年之际去看望灾区小学的小朋友,他们自发捐款准备买点礼品.市场上有大、小两种礼盒套装,若买3大盒4小盒需要76元,若买2大盒3小盒需要54元.
(1)每个大礼盒、小礼盒的价格各是多少元?
(2)如果他们计划买大、小两种礼盒共40盒,要求买的大礼盒比小礼盒多,且购买礼品的总价格不超过捐款总数445元,则有哪几种购买方案?
解:(1)设大礼盒x元/个,小礼盒y元/个,由题意可列方程组如下:
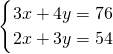
,
解此方程组得x=12,y=10.
即大礼盒12元/个,小礼盒10元/个.
(2)设需买x个大礼盒,则买小礼盒(40-x)个,
由题意可列不等式组:
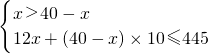
解此不等式组得20<x≤22.5.
因为x是整数,∴x=21,22.
即有两种购买方案:买大礼盒21个,小礼盒19个;买大礼盒22个,小礼盒18个.
分析:(1)设大礼盒x元/个,小礼盒y元/个,则根据“买3大盒4小盒需要76元,买2大盒3小盒需要54元”得到方程组,求方程组的解即可;
(2)设需买x个大礼盒,则买小礼盒(40-x)个,则根据“要求买的大礼盒比小礼盒多,且购买礼品的总价格不超过捐款总数445元”得不等式组,求不等式组的解即可.
点评:解决问题的关键是读懂题意,依题意列出不等式进行求解.

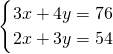 ,
,