
【题目】如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.
(1)请用无刻度的直尺和圆规,过点B作直线m⊥l,交⊙O于C、D(点D在点C的上方);(保留作图痕迹,不要求写作法)
(2)求BC的长.

【答案】(1)答案见解析;(2)2.
【解析】试题分析:(1)利用基本作图(过一点作已知直线的垂线)作直线m得到CD;
(2)作OH⊥CD于H,连接OA、OD,如图,利用垂径定理得到DH=CH,则根据切线的性质得OA⊥l,易得四边形OABH为正方形,所以OH=AB=4,BH=OA=5,然后利用勾股定理计算出DH=3,则CH=3,所以BC=BH﹣CH=2.
试题解析:解:(1)如图,CD为所作;
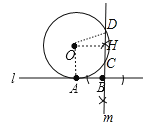
(2)作OH⊥CD于H,连接OA、OD,如图,则DH=CH.∵直线l切⊙O于A,∴OA⊥l,易得四边形OABH为正方形,∴OH=AB=4,BH=OA=5.在Rt△ODH中,DH=![]() =3,∴CH=3,∴BC=BH﹣CH=5﹣3=2.
=3,∴CH=3,∴BC=BH﹣CH=5﹣3=2.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题原型】如图1,在四边形ABCD中,∠ADC=90°,AB=AC.点E、F分别为AC、BC的中点,连结EF,DE.试说明:DE=EF.
【探究】如图2,在问题原型的条件下,当AC平分∠BAD,∠DEF=90°时,求∠BAD的大小.
【应用】如图3,在问题原型的条件下,当AB=2,且四边形CDEF是菱形时,直接写出四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:
13=![]() ×12×22
×12×22
13+23=9=![]() ×22×32
×22×32
13+23+33=36=![]() ×32×42
×32×42
13+23+33+43=100=![]() ×42×52
×42×52
回答下面的问题:
(1)猜想:13+23+33+…+(n-1)3+ n3=________.
(2)利用你得到的(1)中的结论,计算13+23+33+…+993+1003的值.
(3)计算:213+223+…+993+1003的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A、B两点,点A在点B的左侧.
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切?若存在,请求出k的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.
(1)求点E的坐标;
(2)△AEC能否为直角三角形?若能,求出此时抛物线的函数表达式;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(1,m)、Q(n,1)在反比例函数y=![]() 的图象上,直线y=kx+b经过点P、Q,且与x轴、y轴的交点分别为A、B两点.
的图象上,直线y=kx+b经过点P、Q,且与x轴、y轴的交点分别为A、B两点.
(1)求 k、b的值;
(2)O为坐标原点,C在直线y=kx+b上且AB=AC,点D在坐标平面上,顺次联结点O、B、C、D的四边形OBCD满足:BC∥OD,BO=CD,求满足条件的D点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,ABCD为正方形,将正方形的边CB绕点C顺时针旋转到CE,记∠BCE=α,连接BE,DE,过点C作CF⊥DE于F,交直线BE于H.
(1)当α=60°时,如图1,则∠BHC= ;
(2)当45°<α<90°,如图2,线段BH、EH、CH之间存在一种特定的数量关系,请你通过探究,写出这个关系式: (不需证明);
(3)当90°<α<180°,其它条件不变(如图3),(2)中的关系式是否还成立?若成立,说明理由;若不成立,写出你认为成立的结论,并简要证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五张正面分别写有数字﹣2,﹣1,0,1,2的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不大于1的概率是 ;
(2)先从中任意抽取一张卡片,以其正面数字作为a的值,然后再从剩余的卡片随机抽一张,以其正面的数字作为b的值,请用列表法或画树状图法,求点Q(a,b)在第二象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com