
”¾ĢāÄæ”æ”÷ABCŹĒŅ»ÕŵČŃüÖ±½ĒČż½ĒŠĪÖ½°å£¬”ĻC=Rt”Ļ£¬AC=BC=2£¬
£Ø1£©ŅŖŌŚÕāÕÅÖ½°åÖŠ¼ō³öŅ»øö¾”æÉÄÜ“óµÄÕż·½ŠĪ£¬ÓŠ¼×”¢ŅŅĮ½ÖÖ¼ō·Ø£ØČēĶ¼1£©£¬±Č½Ļ¼×”¢ŅŅĮ½ÖÖ¼ō·Ø£¬ÄÄÖÖ¼ō·ØĖłµĆµÄÕż·½ŠĪĆ껿“ó£æĒėĖµĆ÷ĄķÓÉ£®
£Ø2£©Ķ¼1ÖŠ¼×ÖÖ¼ō·Ø³ĘĪŖµŚ1“Ī¼ōČ”£¬¼ĒĖłµĆÕż·½ŠĪĆ껿ĪŖs1£»°“ÕÕ¼×ÖÖ¼ō·Ø£¬ŌŚÓąĻĀµÄ”÷ADEŗĶ”÷BDFÖŠ£¬·Ö±š¼ōČ”Õż·½ŠĪ£¬µĆµ½Į½øöĻąĶ¬µÄÕż·½ŠĪ£¬³ĘĪŖµŚ2“Ī¼ōČ”£¬²¢¼ĒÕāĮ½øöÕż·½ŠĪĆ껿ŗĶĪŖs2£ØČēĶ¼2£©£¬Ōņs2=![]() £»ŌŁŌŚÓąĻĀµÄĖÄøöČż½ĒŠĪÖŠ£¬ÓĆĶ¬Ńł·½·Ø·Ö±š¼ōČ”Õż·½ŠĪ£¬µĆµ½ĖÄøöĻąĶ¬µÄÕż·½ŠĪ£¬³ĘĪŖµŚ3“Ī¼ōČ”£¬²¢¼ĒÕāĖÄøöÕż·½ŠĪĆ껿ŗĶĪŖs3£¬¼ĢŠų²Ł×÷ĻĀČ„”£¬ŌņµŚ10“Ī¼ōČ”Ź±£¬s10=
£»ŌŁŌŚÓąĻĀµÄĖÄøöČż½ĒŠĪÖŠ£¬ÓĆĶ¬Ńł·½·Ø·Ö±š¼ōČ”Õż·½ŠĪ£¬µĆµ½ĖÄøöĻąĶ¬µÄÕż·½ŠĪ£¬³ĘĪŖµŚ3“Ī¼ōČ”£¬²¢¼ĒÕāĖÄøöÕż·½ŠĪĆ껿ŗĶĪŖs3£¬¼ĢŠų²Ł×÷ĻĀČ„”£¬ŌņµŚ10“Ī¼ōČ”Ź±£¬s10=![]() £»
£»
£Ø3£©ĒóµŚ10“Ī¼ōČ”ŗó£¬ÓąĻĀµÄĖłÓŠŠ”Čż½ĒŠĪµÄĆ껿֮ŗĶ£®
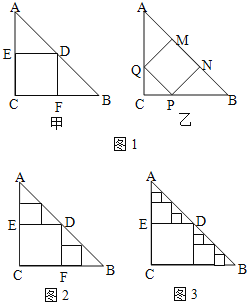
”¾“š°ø”æ½ā£ŗ£Ø1£©½ā·Ø1£ŗČēĶ¼¼×£¬ÓÉĢāŅā£¬µĆAE=DE=EC£¬¼“EC=1£¬SÕż·½ŠĪCFDE=12=1
ČēĶ¼ŅŅ£¬ÉčMN=x£¬ŌņÓÉĢāŅā£¬µĆAM=MQ=PN=NB=MN=x£¬
”ą![]() £¬
£¬
½āµĆ![]()
”ą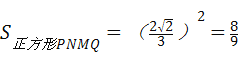
ÓÖ”ß![]()
”ą¼×ÖÖ¼ō·ØĖłµĆµÄÕż·½ŠĪĆ껿øü“ó£®
ĖµĆ÷£ŗĶ¼¼×æÉĮķ½āĪŖ£ŗÓÉĢāŅāµĆµćD”¢E”¢F·Ö±šĪŖAB”¢AC”¢BCµÄÖŠµć£¬SÕż·½ŠĪOFDE=1£®
½ā·Ø2£ŗČēĶ¼¼×£¬ÓÉĢāŅāµĆAE=DE=EC£¬¼“EC=1£¬
ČēĶ¼ŅŅ£¬ÉčMN=x£¬ŌņÓÉĢāŅāµĆAM=MQ=QP=PN=NB=MN=x£¬
”ą![]() £¬
£¬
½āµĆ![]() £¬
£¬
ÓÖ”ß![]() £¬¼“EC£¾MN£®
£¬¼“EC£¾MN£®
”ą¼×ÖÖ¼ō·ØĖłµĆµÄÕż·½ŠĪĆ껿øü“ó£®
£Ø2£©![]() £¬
£¬![]() £®
£®
£Ø3£©½ā·Ø1£ŗĢ½Ė÷¹ęĀÉæÉÖŖ£ŗ![]()
Ź£ÓąČż½ĒŠĪĆ껿ŗĶĪŖ![]() =
=![]()
½ā·Ø2£ŗÓÉĢāŅāæÉÖŖ£¬
µŚŅ»“Ī¼ōČ”ŗóŹ£ÓąČż½ĒŠĪĆ껿ŗĶĪŖ2©S1=1=S1
µŚ¶ž“Ī¼ōČ”ŗóŹ£ÓąČż½ĒŠĪĆ껿ŗĶĪŖ![]() £¬
£¬
µŚČż“Ī¼ōČ”ŗóŹ£ÓąČż½ĒŠĪĆ껿ŗĶĪŖ![]() £¬
£¬
”
µŚŹ®“Ī¼ōČ”ŗóŹ£ÓąČż½ĒŠĪĆ껿ŗĶĪŖ![]() £®
£®
”¾½āĪö”æĀŌ


 ĆæČÕ10·ÖÖÓæŚĖćŠÄĖćĖŁĖćĢģĢģĮ·ĻµĮŠ“š°ø
ĆæČÕ10·ÖÖÓæŚĖćŠÄĖćĖŁĖćĢģĢģĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
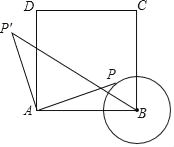
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪABCDÖŠ£¬AB£½3cm£¬ŅŌBĪŖŌ²ŠÄ£¬1cm³¤ĪŖ°ė¾¶»”ŃB£¬µćPŌŚ”ŃBÉĻŅĘ¶Æ£¬Į¬½ÓAP£¬²¢½«APČʵćAÄꏱÕėŠż×Ŗ90”ćÖĮAP”䣬Į¬½ÓBP”䣮ŌŚµćPŅĘ¶ÆµÄ¹ż³ĢÖŠ£¬BP”䳤¶ČµÄ×īŠ”ÖµĪŖ_____cm£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ØŅå£ŗŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ö±Ļßy£½a£Øx©m£©+k³ĘĪŖÅ×ĪļĻßy£½a£Øx©m£©2+kµÄ¹ŲĮŖÖ±Ļߣ®
£Ø1£©ĒóÅ×ĪļĻßy£½x2+6x©1µÄ¹ŲĮŖÖ±Ļߣ»
£Ø2£©ŅŃÖŖÅ×ĪļĻßy£½ax2+bx+cÓėĖüµÄ¹ŲĮŖÖ±Ļßy£½2x+3¶¼¾¹żyÖįÉĻĶ¬Ņ»µć£¬ĒóÕāĢõÅ×ĪļĻߵıķ“ļŹ½£»
£Ø3£©ČēĶ¼£¬¶„µćŌŚµŚŅ»ĻóĻŽµÄÅ×ĪļĻßy£½©a£Øx©1£©2+4aÓėĖüµÄ¹ŲĮŖÖ±Ļß½»ÓŚµćA£¬B£ØµćAŌŚµćBµÄ×ó²ą£©£¬ÓėxÖįøŗ°ėÖį½»ÓŚµćC£¬Į¬½įAC”¢BC£®µ±”÷ABCĪŖÖ±½ĒČż½ĒŠĪŹ±£¬ĒóaµÄÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
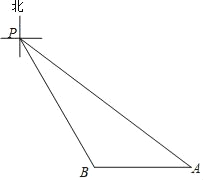
”¾ĢāÄæ”æČēĶ¼£¬PµćŹĒijŗ£ÓņÄŚµÄŅ»×łµĘĖžµÄĪ»ÖĆ£¬“¬AĶ£²“ŌŚµĘĖžPµÄÄĻĘ«¶«53”ć·½ĻņµÄ50ŗ£Ąļ“¦£¬“¬BĪ»ÓŚ“¬AµÄÕżĪ÷·½ĻņĒŅÓėµĘĖžPĻą¾ą20![]() ŗ£Ąļ£®(±¾Ģā²Īæ¼Źż¾Żsin53”ć”Ö0.80£¬cos53”ć”Ö0.60£¬tan53”ć”Ö1.33£®)
ŗ£Ąļ£®(±¾Ģā²Īæ¼Źż¾Żsin53”ć”Ö0.80£¬cos53”ć”Ö0.60£¬tan53”ć”Ö1.33£®)
(1)ŹŌĪŹ“¬BŌŚµĘĖžPµÄŹ²Ć“·½Ļņ£æ
(2)ĒóĮ½“¬Ļą¾ą¶ąÉŁŗ£Ąļ£æ(½į¹ū±£ĮōøłŗÅ)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ĘĖć
(1)x2+6x©2£½0(Åä·½·Ø)
(2)ŅŃÖŖ¹ŲÓŚxµÄ·½³Ģ2x2+(k©2)x+1£½0ÓŠĮ½øöĻąµČµÄŹµŹżøł£¬ĒókµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ŹĒŅ»øöŃü³¤ĪŖ4cm£¬µ×±ß³¤ĪŖ3cmµÄµČŃüČż½ĒŠĪ£¬ĻÖŌŚŅŖĄūÓĆÕāøöµČŃüČż½ĒŠĪ¼Ó¹¤³öŅ»øö±ß³¤±ČŹĒ1£ŗ2µÄĘ½ŠŠĖıߊĪ£¬Ź¹Ę½ŠŠĖıߊĪµÄŅ»øöÄŚ½ĒĒ”ŗĆŹĒÕāøöµČŃüČż½ĒŠĪµÄµ×½Ē£¬Ę½ŠŠĖıߊĪµÄĘäĖū¶„µć¾łŌŚČż½ĒŠĪµÄ±ßÉĻ£¬ŌņÕāøöĘ½ŠŠĖıߊĪµÄ½Ļ¶ĢµÄ±ß³¤ŹĒ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
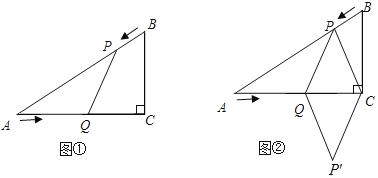
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼¢Ł£¬ŌŚRt”÷ABCÖŠ£¬”ĻC£½90”ć£¬AC£½8cm£¬BC£½6cm£¬µćPÓÉB³ö·¢ŃŲBA·½ĻņĻņµćAŌČĖŁŌĖ¶Æ£¬ĖŁ¶ČĪŖ1cm/s£»µćQÓÉA³ö·¢ŃŲAC·½ĻņĻņµćCŌČĖŁŌĖ¶Æ£¬ĖŁ¶ČĪŖ2cm/s£»Į¬½ÓPQ£®ČōÉčŌĖ¶ÆµÄŹ±¼äĪŖt£Øs£©£Ø0£¼t£¼4£©£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©µ±tĪŖŗĪÖµŹ±£¬PQ”ĪBC£»
£Ø2£©Éč”÷AQPµÄĆ껿ĪŖy£Øcm2£©£¬ĒóyÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©ŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢt£¬Ź¹Ļ߶ĪPQĒ”ŗĆ°ŃRt”÷ACBµÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö£æČō“ęŌŚ£¬Ēó³ö“ĖŹ±tµÄÖµ£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£»
£Ø4£©ČēĶ¼¢Ś£¬Į¬½ÓPC£¬²¢°Ń”÷PQCŃŲQC·ÕŪ£¬µĆµ½ĖıߊĪPQP”äC£¬ÄĒĆ“ŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢt£¬Ź¹ĖıߊĪPQP”äCĪŖĮāŠĪ£æČō“ęŌŚ£¬Ēó³ö“ĖŹ±ĮāŠĪµÄ±ß³¤£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¾ŲŠĪABCDŗĶ¾ŲŠĪEFGOŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćB£¬FµÄ×ų±ź·Ö±šĪŖ(£4,4)£¬(2,1)£®Čō¾ŲŠĪABCDŗĶ¾ŲŠĪEFGOŹĒĪ»ĖĘĶ¼ŠĪ£¬µćP(µćPŌŚGCÉĻ)ŹĒĪ»ĖĘÖŠŠÄ£¬ŌņµćPµÄ×ų±źĪŖ(””””)
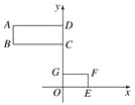
A. (0,3)
B. (0,2.5)
C. (0,2)
D. (0,1.5)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”õABCDµÄ¶Ō½ĒĻßĻą½»ÓŚµćO£¬µćEŌŚ±ßBCµÄŃÓ³¤ĻßÉĻ£¬ĒŅOE=OB£¬Į¬½ÓDE£®

£Ø1£©ĒóÖ¤£ŗDE”ĶBE£»
£Ø2£©Čē¹ūOE”ĶCD£¬ĒóÖ¤£ŗBD”¤CE=CD”¤DE£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com