Question

6．如图，已知直线a∥b，直线m和直线a、b交于点C和D，点A在直
线a上，点B在直线b上，点P在直线m上，且点A、B的位置不变，记∠PAC=α，∠APB=β，∠PBD=γ．
（1）当点P在C、D之间运动时，问α、β、γ之间有什么数量关系？请说明理由．
（2）当点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索α、β、γ之间的数量关系是β=γ-α或β=α-γ（直接写出答案）．

Answer 1

分析 （1）过P点做PQ∥a，根据两直线平行，内错角相等即可证得；
（2）当点P在C点外侧运动时，过P点做PQ∥a，根据两直线平行，内错角相等即可证得；当点P在D点外侧运动时，同理可证得．

解答 解：（1）β=α+γ，
如图1，过点P作PQ∥a，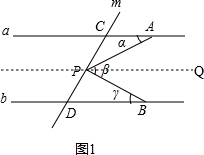

∴∠APQ=∠PAC=α，
又∵a∥b，
∴PQ∥b，
∴∠BPQ=∠PBD=γ，
∵∠APB=∠APQ+∠BPQ，
∴β=α+γ；

（2）如图2，当点P在C点外侧运动时，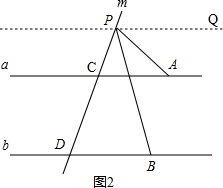

过P点做PQ∥a．
∵a∥b，
∴PQ∥a∥b，
∴∠APQ=∠PAC，∠QPB=∠PBD，
∴∠QPB-∠QPA=∠PBD-∠PAC，
∵∠QPB-∠QPA=∠APB，
∴∠APB=∠PBD-∠PAC，即β=γ-α；
如图3，当点P在D点外侧运动时，过P点做PM∥a，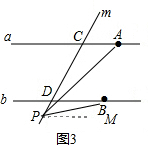

∵a∥b，
∴PM∥a∥b，
∴∠APM=∠PAC，∠MPB=∠PBD，
∴∠MPA-∠MPB=∠PAC-∠PBD，
∵∠MPA-∠MPB=∠APB，
∴∠APB=∠PAC-∠PBD，即β=α-γ，
故答案为：β=γ-α或β=α-γ．

点评 本题利用了平行线的性质：两直线平行，内错角相等，正确作出辅助线，以及注意（2）中分情况讨论是关键．