
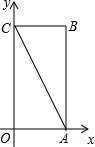
 别与x轴、y轴重合,折叠该纸,折痕与边OC交于点D,与对角线AC交于点M,
别与x轴、y轴重合,折叠该纸,折痕与边OC交于点D,与对角线AC交于点M,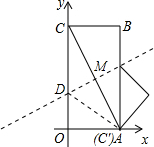 解:(1)由题意得点M是AC的中点,点A(2,0)点C(0,4),
解:(1)由题意得点M是AC的中点,点A(2,0)点C(0,4),| 5 |
| 5 |
| 1 |
| 8 |
| 1 |
| 8 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
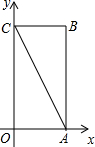 别与x轴、y轴重合,折叠该纸,折痕与边OC交于点D,与对角线AC交于点M,
别与x轴、y轴重合,折叠该纸,折痕与边OC交于点D,与对角线AC交于点M,查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(天津市卷)数学(带解析) 题型:解答题
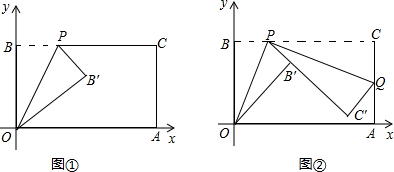
已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.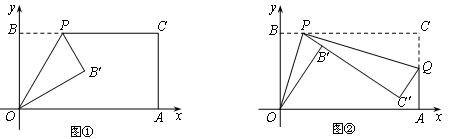
(Ⅰ)如图①,当∠BOP=300时,求点P的坐标;
(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;
(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-相似的判定解答题(解析版) 题型:解答题
已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.

(Ⅰ)如图①,当∠BOP=30°时,求点P的坐标;
(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;
(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com