


|


科目:初中数学 来源: 题型:
| A、60.02×105 |
| B、6.002×106 |
| C、6.002×102 |
| D、6.002×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,AB和AC是夹角为127°的两面水泥墙俯视图,其中AB墙长为5米,AC墙长为15米,现借用这两面墙,并用16米长的篱笆(图中线段DE,EF的长度和)作另两面墙,围成一个四边形菜园ADEF,使得DE∥AC,DE⊥EF.设EF的长为x米,菜园ADEF的面积为y平方米.
已知,如图,AB和AC是夹角为127°的两面水泥墙俯视图,其中AB墙长为5米,AC墙长为15米,现借用这两面墙,并用16米长的篱笆(图中线段DE,EF的长度和)作另两面墙,围成一个四边形菜园ADEF,使得DE∥AC,DE⊥EF.设EF的长为x米,菜园ADEF的面积为y平方米.查看答案和解析>>
科目:初中数学 来源: 题型:
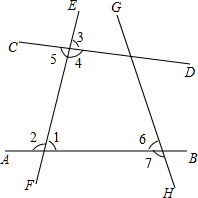 如图,直线AB、CD被直线EF所截,在所标出的角中,那几对角是同位角?哪几对是内错角?哪几对是同旁内角?类似地,类似地,你能讨论直线EF、GH被直线AB所截形成的角的位置关系吗?
如图,直线AB、CD被直线EF所截,在所标出的角中,那几对角是同位角?哪几对是内错角?哪几对是同旁内角?类似地,类似地,你能讨论直线EF、GH被直线AB所截形成的角的位置关系吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com