
【题目】(12分)在等腰△ABC中,AB=AC=2, ∠BAC=120°,AD⊥BC于D,点O、点P分别在射线AD、BA上的运动,且保证∠OCP=60°,连接OP.
(1)当点O运动到D点时,如图一,此时AP=______,△OPC是什么三角形。
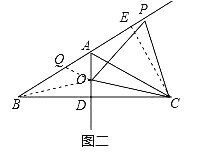
(2)当点O在射线AD其它地方运动时,△OPC还满足(1)的结论吗?请用利用图二说明理由。
(3)令AO=x,AP=y,请直接写出y关于x的函数表达式,以及x的取值范围。
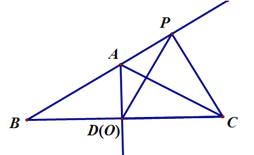
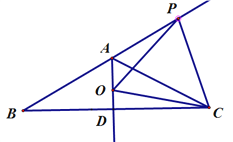
图一 图二
【答案】(1)1,等边三角形;(2)理由见解析;(3)当![]() 时,y=2-x;当
时,y=2-x;当![]() 时,
时,
y=x-2
【解析】试题分析:(1)根据等腰三角形的性质得到∠B=∠ACB=30°,求得∠ACP=30°,根据全等三角形的性质即可得到结论;(2)过C作CE⊥AP于E,根据等边三角形的性质得到CD=CE,根据全等三角形的性质得到OC=OP,由等边三角形的判定即可得到结论;(3)分两种情况解决,在AB上找到Q点使得AQ=OA,则△AOQ为等边三角形,根据求得解实现的性质得到PA=BQ,求得AC=AO+AP,即可得到结论.
试题解析:
(1)AD=AP=1,
∵AB=AC=2,∠BAC=120°,
∴∠B=∠ACB=30°,
∵∠OCP=60°,
∴∠ACP=30°,
∵∠CAP=180°﹣∠BAC=60°,
∵AD⊥BC,
∴∠DAC=60°,
在△ADC与△APC中, 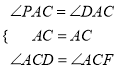 ,
,
∴△ACD≌△ACP,
∴CD=CP,
∴△PCO是等边三角形;
(2)△OPC还满足(1)的结论,
理由:过C作CE⊥AP于E,
∵∠CAD=∠EAC=60°,
AD⊥CD,
∴CD=CE,
∴∠DCE=60°,
∴∠OCE=∠PCE,
在△OCD与△PCE中, 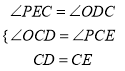 ,
,
∴△OCD≌△PCE,
∴OC=OP,
∴△OPC是等边三角形;
(3)当0<x≤2时,
在AB上找到Q点使得AQ=OA,则△AOQ为等边三角形,
则∠BQO=∠PAO=120°,
在△BQO和△PAO中, 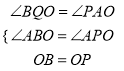 ,
,
∴△BQO≌△PAO(AAS),
∴PA=BQ,
∵AB=BQ+AQ,
∴AC=AO+AP,
∵AO=x,AP=y,
∴y=﹣x+2;
当![]() 时, 利用同样的方法可求得y=x-2
时, 利用同样的方法可求得y=x-2


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】一个长80cm,宽70cm的矩形铁皮,将四个角各剪去一个边长为xcm的小正方形后,剩余部分刚好围成一个底面积为3000cm2的无盖长方体盒子,求小正方形边长xcm时,可根据下列方程( )
A. (80﹣x)(70﹣x)=3000 B. (80﹣2x)(70﹣2x)=3000
C. 80×70﹣4x2=3000 D. 80×70﹣4x2﹣(80+70)x=3000
查看答案和解析>>
科目:初中数学 来源: 题型:
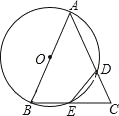
【题目】(2016宁夏第23题)已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县“果菜大王”王大炮收货番茄20吨,青椒12吨.现计划租用甲、乙两种货车共8辆将这批果菜全部运往外地销售,已知一辆甲种货车可装番茄4吨和青椒1吨,一辆乙种货车可装番茄和青椒各2吨.
(1)王灿有几种方案安排甲、乙两种货车可一次性地将果菜运到销售地?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王大炮应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑3 000元,购买1台学习机800元.
(1)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168 000元,则购买平板电脑最多多少台?
(2)在(1)的条件下,购买学习机的台数不超过平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com