
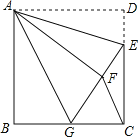
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
①△ABG≌△AFG;② BG=GC;③ AG∥CF;④∠GAE=45°.
则正确结论的个数有( )
A. 1B. 2C. 3D. 4
【答案】D
【解析】
根据正方形的性质得出AB=AD=DC=6,∠B=D=90°,求出DE=2,AF=AB,根据HL推出Rt△ABG≌Rt△AFG,推出BG=FG,∠AGB=∠AGF,设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2,在Rt△ECG中,由勾股定理得出(6-x)2+42=(x+2)2,求出x=3,得出BG=GF=CG,求出∠AGB=∠FCG,推出AG∥CF,根据全等得出∠DAE=∠FAE,∠BAG=∠FAG.
解:∵四边形ABCD是正方形,
∴AB=AD=DC=6,∠B=D=90°,
∵CD=3DE,
∴DE=2,
∵△ADE沿AE折叠得到△AFE,
∴DE=EF=2,AD=AF,∠D=∠AFE=∠AFG=90°,
∴AF=AB,
∵在Rt△ABG和Rt△AFG中
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL).
∴①正确;
∵Rt△ABG≌Rt△AFG,
∴BG=FG,∠AGB=∠AGF.
设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2.在Rt△ECG中,由勾股定理得:CG2+CE2=EG2.
∵CG=6-x,CE=4,EG=x+2,
∴(6-x)2+42=(x+2)2,解得:x=3.
∴BG=GF=CG=3.
∴②正确;
∵CG=GF,
∴∠CFG=∠FCG.
∵∠BGF=∠CFG+∠FCG,∠BGF=∠AGB+∠AGF,
∴∠CFG+∠FCG=∠AGB+∠AGF.
∵∠AGB=∠AGF,∠CFG=∠FCG,
∴∠AGB=∠FCG.
∴AG∥CF.
∴③正确;
∵△ADE沿AE折叠得到△AFE,
∴△DAE≌△FAE.
∴∠DAE=∠FAE.
∵△ABG≌△AFG,
∴∠BAG=∠FAG.
∵∠BAD=90°,
∴∠EAG=∠EAF+∠GAF=![]() ×90°=45°.
×90°=45°.
∴④正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度,已知烈山坡面与水平面的夹角为30°,山高857.5尺,组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点,在点E处测得雕像顶端A的仰角为60°,求雕像AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α﹣90°;②∠EOB=180°﹣α;③∠AOF=360°﹣2α,其中正确的是( )
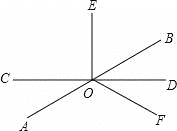
A. ①②B. ①③C. ②③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
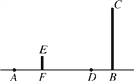
【题目】如图,在一座大厦(图中BC所示)前面30m的地面上,有一盏地灯A照射大厦,身高为1.6m的小亮(图中EF所示)站在大厦和灯之间,若小亮从现在所处位置径直走向大厦,当他走到距离大厦只有5m的D处时停下.
(1)请在图中画出此时小亮的位置(可用线段表示)及他在地灯照射下投在大厦BC上的影子;
(2)请你求出此时小亮的影长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题中选择一个,七年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.
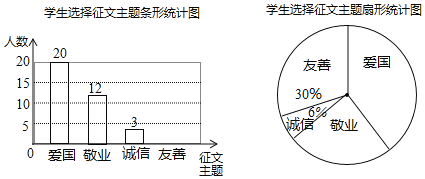
(1)将上面的条形统计图补充完整;
(2)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少度?
(3)如果该校七年级共有1200名考生,请估计选择以“友善”为主题的七年级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬“雷锋精神”,我县开展“做雷锋精神种子.当四品八德少年”主题征文比赛,已知每篇参赛征文成绩记![]() 分(
分(![]() ) ,组委会从
) ,组委会从![]() 篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
县主题征文比赛成绩频数分布表
分数段 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
县主题征文比赛成绩频数分布直方图
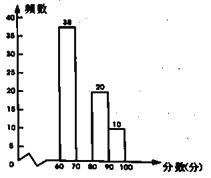
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中![]() 的值是 ;
的值是 ;
(2)补全征文比赛成绩频数分布直方图:
(3)若![]() 分以上(含
分以上(含![]() 分)的征文将被评为一等奖,请估算全县获得一等奖征文的篇数.
分)的征文将被评为一等奖,请估算全县获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海船以5海里/小时的速度向正东方向行驶,在A处看见灯塔B在海船的北偏东60°方向,2小时后船行驶到C处,发现此时灯塔B在海船的北偏西45°方向,求此时灯塔B到C处的距离。
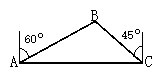
查看答案和解析>>
科目:初中数学 来源: 题型:
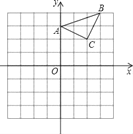
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1.
(2)点C1的坐标为( , ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com