
 Ϊ�˽⡰�����У�����չ�����ij��ѧ���������ν����˶������Ų��ԣ�ÿ������5�Σ����а༶���Խ����������ȡ��ij��ѧ�������������Ϊ�������Խ���������������������˲�������ͳ��ͼ�����ð�Ů����22�ˣ�Ů���������������Ϊ2����λ��Ϊ3��
Ϊ�˽⡰�����У�����չ�����ij��ѧ���������ν����˶������Ų��ԣ�ÿ������5�Σ����а༶���Խ����������ȡ��ij��ѧ�������������Ϊ�������Խ���������������������˲�������ͳ��ͼ�����ð�Ů����22�ˣ�Ů���������������Ϊ2����λ��Ϊ3��| �������������� | ������ |
| ��0 | ��1 |
| ��1 | ��2 |
| ��2 | ��x |
| ��3 | ��y |
| ��4 | ��4 |
| ��5 | ��2 |
���� ��1�����ݽ�����Ϊ3������������ռ�İٷֱ�����������������ɣ����������Ϊ4�����������Լ�������Ϊ2����Բ�ĽǶ�������ȫ����ͳ��ͼ���ɣ�
��2��������ã�x+y=22-1-2-4-2=13������Ů���������������Ϊ2����λ��Ϊ3�����ǵõ����ۣ�
��3�����������������3���İٷֱȣ�����1880���ɵõ������
��� �⣺��1������༶����������Ϊ6��24%=25���ˣ���
������༶����������Ϊ25�ˣ�����������Ϊ4��������Ϊ25-��1+2+5+6+4��=7���ˣ�����2���������Բ�ĽǶ���Ϊ360���$\frac{2}{25}$=72�㣻
��ȫ����ͳ��ͼ����ͼ��ʾ��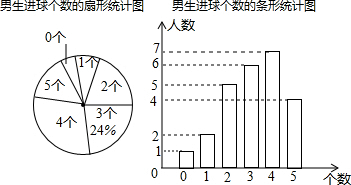
��2��������ã�x+y=22-1-2-4-2=13��
��nŮ���������������Ϊ2����λ��Ϊ3��
��x=7��y=6��
��3����������ã�47��ѧ����Ů���������Ϊ6+4+2=12������������Ϊ6+7+4=17��
��1880��$\frac{12+17}{47}$=1160���ˣ���
��ȫУ������������3����ѧ����Լ��1160�ˣ�
���� ���⿼��������ͳ��ͼ������ͳ��ͼ���������������壬Ū�����е������ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
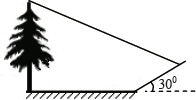 С�����һ�����ĸ߶ȣ�����������Ӱ��ǡ�����ڵ����һб���ϣ���ͼ����ʱ��õ����ϵ�Ӱ��Ϊ16�ף������ϵ�Ӱ��Ϊ8�ף���֪б�µ��½�Ϊ30�㣬ͬһʱ�̣�һ����Ϊ1�ס���ֱ�ڵ�����õı���ڵ����ϵ�Ӱ��Ϊ2�ף������ĸ߶�Ϊ��������
С�����һ�����ĸ߶ȣ�����������Ӱ��ǡ�����ڵ����һб���ϣ���ͼ����ʱ��õ����ϵ�Ӱ��Ϊ16�ף������ϵ�Ӱ��Ϊ8�ף���֪б�µ��½�Ϊ30�㣬ͬһʱ�̣�һ����Ϊ1�ס���ֱ�ڵ�����õı���ڵ����ϵ�Ӱ��Ϊ2�ף������ĸ߶�Ϊ��������| A�� | 12+2$\sqrt{3}$�� | B�� | 24�� | C�� | 8+4$\sqrt{3}$�� | D�� | 20�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
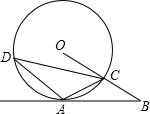 ��֪����ͼ��A�ǡ�O��һ�㣬�뾶OC���ӳ��������A��ֱ�߽���B�㣬OC=BC��AC=$\frac{1}{2}$OB��
��֪����ͼ��A�ǡ�O��һ�㣬�뾶OC���ӳ��������A��ֱ�߽���B�㣬OC=BC��AC=$\frac{1}{2}$OB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com