
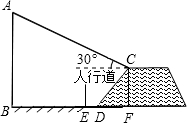
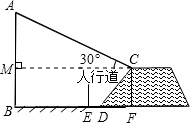
 解:如图,作CM⊥AB于点M,则MBFC为矩形.
解:如图,作CM⊥AB于点M,则MBFC为矩形.| CF |
| DF |
| 2 |
| 1 |
| 1 |
| 2 |
| AM |
| CM |
| ||
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
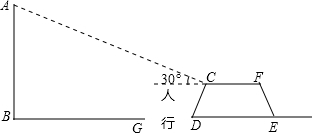
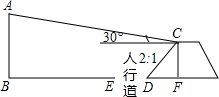 城市规划期间,欲拆除一电线杆AB(如图),已知距电线杆AB水平距离14m的D处有一大坝,背水坝CD的坡度i=2:1,坝高CF为2m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道,试问在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上,请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域)(
城市规划期间,欲拆除一电线杆AB(如图),已知距电线杆AB水平距离14m的D处有一大坝,背水坝CD的坡度i=2:1,坝高CF为2m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道,试问在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上,请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域)(| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 时,为确保安全是否将此行车道封上?请说明理由.
时,为确保安全是否将此行车道封上?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
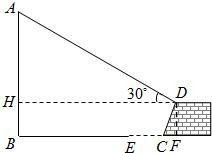
 我市城市规划期间,欲拆除沿江路一电线杆AB(如图),已知望月堤D距电线杆AB水平距离为14m,背水面CD的坡度i=2:1,堤高CF为2m,在堤顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道,试问在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上,请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域)(
我市城市规划期间,欲拆除沿江路一电线杆AB(如图),已知望月堤D距电线杆AB水平距离为14m,背水面CD的坡度i=2:1,堤高CF为2m,在堤顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道,试问在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上,请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域)(| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com