Question

20．有一张等腰三角形纸片，AB=AC=5，BC=3，小明将它沿虚线PQ剪开，得到△AQP和四边形BCPQ两张纸片（如图所示），且满足∠BQP=∠B，则下列五个数据$\frac{15}{4}$，3，$\frac{16}{5}$，2，$\frac{5}{3}$中可以作为线段AQ长的有3个．

Answer 1

分析 作CD∥PQ，交AB于D，由平行线的性质和等腰三角形的性质得出∠B=∠ACB=∠CDB，证出CD=BC=3，△BCD∽△BAC，得出对应边成比例求出BD=$\frac{9}{5}$，得出AD=AB-BD=$\frac{16}{5}$，由平行线证出△APQ∽△ACD，得出对应边成比例求出AP=$\frac{25}{16}$AQ，再分别代入AQ的长求出AP的长，即可得出结论．

解答 解：作CD∥PQ，交AB于D，如图所示：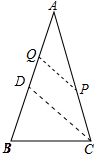
则∠CDB=∠BQP，
∵AB=AC=5，
∴∠B=∠ACB，
∵∠BQP=∠B，
∴∠B=∠ACB=∠CDB，
∴CD=BC=3，△BCD∽△BAC，
∴$\frac{BC}{AB}=\frac{BD}{BC}$，即$\frac{3}{5}=\frac{BD}{3}$，
解得：BD=$\frac{9}{5}$，
∴AD=AB-BD=$\frac{16}{5}$，
∵CD∥PQ，
∴△APQ∽△ACD，
∴$\frac{AP}{AC}=\frac{AQ}{AD}$，即$\frac{AP}{5}=\frac{AQ}{\frac{16}{5}}$，
解得：AP=$\frac{25}{16}$AQ，
当AQ=$\frac{15}{4}$时，AP=$\frac{25}{16}$×$\frac{15}{4}$=$\frac{375}{64}$＞5，不合题意，舍去；
当AQ=3时，AP=$\frac{25}{16}$×3=$\frac{75}{16}$＜5，符合题意；
当AQ=$\frac{16}{5}$时，点P与C重合，不合题意，舍去；
当AQ=2时，AP=$\frac{25}{16}$×2=$\frac{50}{16}$＜5，符合题意；
当AQ=$\frac{5}{3}$时，AP=$\frac{25}{16}$×$\frac{5}{3}$=$\frac{125}{48}$＜5，符合题意；
综上所述：可以作为线段AQ长的有3个；
故答案为：3．

点评 本题考查了相似三角形的判定与性质、等腰三角形的判定与性质、平行线的性质；熟练掌握等腰三角形的性质与判定，证明三角形相似是解决问题的关键．