
【题目】如图,在等边△ABC中,过A,B,C三点在三角形内分别作∠1=∠2=∠3,三个角的边相交于D,E,F,

(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明.
(2)△DEF是否为正三角形?请说明理由.
【答案】(1)见解析;(2)见解析;
【解析】
(1)由正三角形的性质得出∠CAB=∠ABC=∠BCA=60°,AB=BC,证出∠ABD=∠BCE,由ASA证明△ABD≌△BCE即可;
(2)由全等三角形的性质得出∠ADB=∠BEC=∠CFA,证出∠FDE=∠DEF=∠EFD,即可得出结论;
(1)∵△ABC是正三角形,
∴∠CAB=∠ABC=∠BCA=60°,AB=BC,
∵∠ABD=∠ABC-∠2,∠BCE=∠ACB-∠3,∠2=∠3,
∴∠ABD=∠BCE,
在△ABD和△BCE中
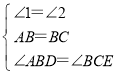 ,
,
∴△ABD≌△BCE(ASA);
(2)△DEF是正三角形;理由如下:
∵△ABD≌△BCE≌△CAF,
∴∠ADB=∠BEC=∠CFA,
∴∠FDE=∠DEF=∠EFD,
∴△DEF是正三角形;


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】问题情境:在综合与实践课上,同学们以“已知三角形三边的长度,求三角形面积”为主题开展数学活动,小颖想到借助正方形网格解决问题。图1、图2都是8×8的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点。
操作发现:小颖在图1中画出△ABC,其顶点A、B、C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE、EF分别经过点C、A,她借助此图求出了△ABC的面积。
(1)在图1中,小颖所画的△ABC的三边长分别是AB= ,BC= ,AC= ;△ABC的面积为 。
(2)请你根据小颖的思路,在图2中以格点为顶点画一个△DEF,使三角形三边长分别为2、![]() 、
、![]() ,并直接写出△DEF的面积= 。
,并直接写出△DEF的面积= 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).
(1)请在图中作出△ABC关于y轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直写出D、E、F的坐标.D、E、F点的坐标是:D( , ) E( , ) F( , );
(2)求四边形ABED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形与中间的小正方形拼成的一个大正方形如果大正方形的面积是13,小正方形的面积是4,直角三角形的较短直角边为a,较长直角边为b,那么![]() 的值为______________.
的值为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与两坐标轴分别交于
的图象与两坐标轴分别交于![]() ,
,![]() ,
,![]() 三点,一次函数的图象与抛物线交于
三点,一次函数的图象与抛物线交于![]() ,
,![]() 两点.
两点.

![]() 求点
求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
![]() 当两函数的函数值都随着
当两函数的函数值都随着![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围;
的取值范围;
![]() 当自变量
当自变量![]() 满足什么范围时,一次函数值大于二次函数值.
满足什么范围时,一次函数值大于二次函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
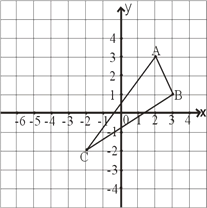
【题目】如图,△ABC中,A、B两个顶点在![]() 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com