
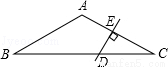
如图,已知: AD是BC上的中线 ,且DF=DE.求证:BE∥CF.(8分)

科目:初中数学 来源:2014-2015学年新疆伊宁市八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图所示,已知在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,DE⊥BC于E,若BC=12 cm,则△DEB的周长为______cm。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省八年级上学期第三次段考数学试卷(解析版) 题型:填空题
(8分)数学课上,李老师出示了如下的题目:
“在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图,试确定线段AE与DB的大小关系,并说明理由”.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论(2分)
当点E为AB的中点时,如图①,确定线段AE与DB的大小关系,请你直接写出结论:
AE ______ DB(填“>”,“<”或“=”).
(2)特例启发,解答题目(4分)
【解析】
题目中,AE与DB的大小关系是:AE _____ DB(填“>”,“<”或“=”).
理由如下:
如图②,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)


(3)拓展结论,设计新题(2分)
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为2,AE=1,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省八年级上学期第三次段考数学试卷(解析版) 题型:选择题
如图,在等腰△ABC中,∠BAC=120°,DE是AC的垂直平分线,线段DE=1cm,则BD的长为 ( )
 .
.
A.6cm B.8cm C .3cm D.4cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安岳池白庙督导区八年级10月月考数学试卷(解析版) 题型:解答题
如图,一个六边形的六个内角都是120°,AB=1,BC=CD=3,DE=2,求该六边形的周长.(8分)
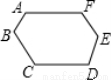
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安岳池白庙督导区八年级10月月考数学试卷(解析版) 题型:填空题
三角形的三边长分别为7,1+2x,13,则x的取值范围是________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年青海师大附属二中八年级上学期第二次月考数学试卷(解析版) 题型:选择题
如图7:AB=AC=BD,则∠1和∠2的关系是( )
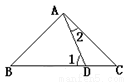
A.∠1=2∠2 B.2∠1+∠2=180o
C.∠1+3∠2=180o D.3∠1-∠2=180o
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com