
分析 先计算括号内分式的加法,再将除法转化为乘法,最后计算乘法即可.
解答 解:原式=[$\frac{{x}^{2}-2x+4}{x-1}$+$\frac{(x-1)(2-x)}{x-1}$]•$\frac{1-x}{(x+2)^{2}}$
=[$\frac{{x}^{2}-2x+4}{x-1}$+$\frac{-{x}^{2}+3x-2}{x-1}$]•$\frac{1-x}{(x+2)^{2}}$
=$\frac{x+2}{x-1}$•$\frac{1-x}{(x+2)^{2}}$
=-$\frac{1}{x+2}$.
故答案为:-$\frac{1}{x+2}$.
点评 本题主要考查分式的混合运算,熟练掌握分式的混合运算顺序和运算法则是解题的关键.


科目:初中数学 来源:2017届重庆市九年级3月月考数学试卷(解析版) 题型:单选题
函数y=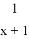 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A. x>-1 B. x<-1 C. x≠-1 D. x≠0
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
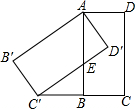 如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E.
如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{\sqrt{2}}$ | D. | -$\frac{1}{\sqrt{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
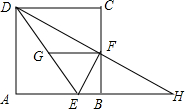 如图,正方形ABCD中,点E在AB上,且BE=$\frac{1}{4}$AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论:
如图,正方形ABCD中,点E在AB上,且BE=$\frac{1}{4}$AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>2 | B. | x≤$\frac{1}{2}$ | C. | x≠$\frac{1}{2}$ | D. | x≤2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com