
 如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).分析 (1)先根据勾股定理求AD的长,从而得BD的长,在Rt△BCD中,计算tan∠B的值即可;
(2)当点M落在BC边上时,如图1,根据AB=5列等式:3t+4t+2t=5,可求得t的值;
(3)分三种情况:
①当0<t≤$\frac{5}{9}$时,如图1,正方形PQMN与△ABC重叠部分是正方形PQMN,
②当$\frac{5}{9}$<t<$\frac{5}{7}$时,如图3,正方形PQMN与△ABC重叠部分是五边形EQPNF,不符合题意;
③当$\frac{5}{7}$≤t<1时,如图4,正方形PQMN与△ABC重叠部分是梯形EQPB,分别计算四边形的面积即可;
(4)分别计算当t=$\frac{5}{7}$和1时,边BC将正方形PQMN的面积分为两部分的面积的比,对比图形写出t的取值.
解答 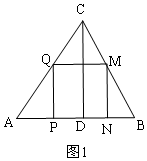 解:(1)∵CD⊥AB,
解:(1)∵CD⊥AB,
∴∠ADC=∠ADB=90°,
∵在Rt△ACD中,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=3,
∴BD=AB-AD=5-3=2,
∴在Rt△BCD中,tan∠B=$\frac{CD}{BD}$=$\frac{4}{2}$=2;
(2)当点M落在BC边上时,如图1,
由题意得:AP=3t,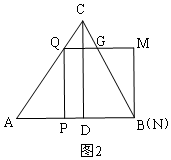
tan∠CAB=$\frac{CD}{AD}=\frac{4}{3}$,
∴PQ=PN=MN=4t,BN=2t,
∴3t+4t+2t=5,
t=$\frac{5}{9}$;
(3)分三种情况:
①当0<t≤$\frac{5}{9}$时,如图1,正方形PQMN与△ABC重叠部分是正方形PQMN,
∴S=PQ2=(4t)2=16t2;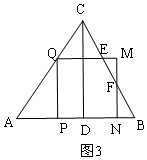
②当N与B重合时,如图2,
AP=3t,PQ=PB=4t,
∴3t+4t=5,
t=$\frac{5}{7}$,
当$\frac{5}{9}$<t<$\frac{5}{7}$时,如图3,正方形PQMN与△ABC重叠部分是五边形EQPNF,
③当$\frac{5}{7}$≤t<1时,如图4,正方形PQMN与△ABC重叠部分是梯形EQPB,
∴AP=3t,PN=4t,
∴BN=7t-5,PB=4t-(7t-5)=-3t+5,
在Rt△APQ中,AQ=5t,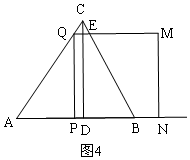
∴QC=5-5t,
∵AC=AB,
∴∠ACB=∠ABC,
∵QE∥AB,
∴∠QEC=∠ABC,
∴∠QEC=∠ACB,
∴QE=QC=5-5t,
∴S=S梯形QPBE=$\frac{1}{2}$(QE+PB)×PQ,
=$\frac{1}{2}$(5-5t+5-3t)×4t=-16t2+20t;
综上所述,S与t之间的函数关系式为:$\left\{\begin{array}{l}{16{t}^{2}(0<t≤\frac{5}{9})}\\{-16{t}^{2}+20t(\frac{5}{7}≤t<1)}\end{array}\right.$.
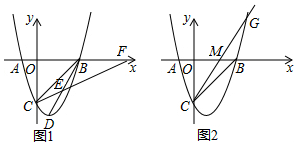
(4)如图2,当t=$\frac{5}{7}$时,CQ=QG=5-5t=$\frac{10}{7}$,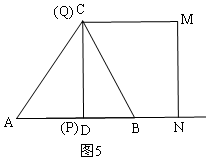
∴GM=4t-$\frac{10}{7}$=$\frac{10}{7}$,
∴QG=GM,
∴S△QGB=S△GMB,
∴S梯形GQPB:S△GMB=3:1,
当P与D重合时,t=1,如图5,
则S△CDB:S四边形CBNM=$\frac{1}{2}$×2×4:(42-$\frac{1}{2}$×2×4),
=1:3,
∴$\frac{5}{9}$<t≤$\frac{5}{7}$,1≤t<$\frac{5}{3}$.
点评 本题是四边形的综合题,考查了正方形的性质、等腰三角形的性质、勾股定理和重叠部分的面积,比较复杂,此类题要先求特殊位置时对应的t值,做到不重不漏,利用数形结合的思想,先确定重叠部分图形的形状,再求其面积.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
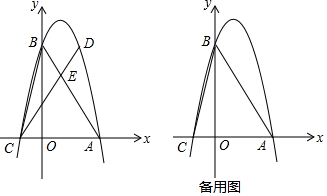
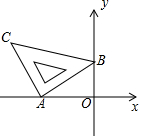 含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的解析式为y=-$\frac{1}{3}$x+1.
含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的解析式为y=-$\frac{1}{3}$x+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )
如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )| A. | (0,1) | B. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | C. | ($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
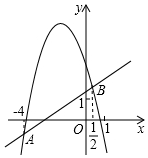 如图,抛物线y1=ax2+bx+c与直线y2=kx+n的图象交于A(-4,-1),B两点,下列判断中:①abc>0;②a+b+c<0;③不等式ax2+bx+c<kx+n的解集为-4<x<$\frac{1}{2}$;④方程ax2+bx+c=-1的解为x=-4,其中正确的个数是( )
如图,抛物线y1=ax2+bx+c与直线y2=kx+n的图象交于A(-4,-1),B两点,下列判断中:①abc>0;②a+b+c<0;③不等式ax2+bx+c<kx+n的解集为-4<x<$\frac{1}{2}$;④方程ax2+bx+c=-1的解为x=-4,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在足球赛中,弱队战胜强队 | |
| B. | 长分别为3、5、9厘米的三条线段能围成一个三角形 | |
| C. | 抛掷一枚硬币,落地后正面朝上 | |
| D. | 任取两个正整数,其和大于1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
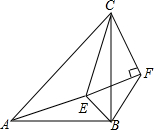 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com