
分析 根据题意画出图形,过D点作DF⊥AB于点F.可求?ABCD和△BCE的高,观察图形可知阴影部分的面积=?ABCD的面积-扇形ADE的面积-△BCE的面积,计算即可求解.
解答  解:如图所示,过D点作DF⊥AB于点F.
解:如图所示,过D点作DF⊥AB于点F.
∵AD=2,AB=4,∠A=45°,
∴DF=AD•sin45°=$\sqrt{2}$,EB=AB-AE=4-2=2,
∴阴影部分的面积=S平行四边形ABCD-S扇形DAE-S△BCE=4$\sqrt{2}$-$\frac{45π×4}{360}$-$\frac{1}{2}$×2×$\sqrt{2}$
=4$\sqrt{2}$-$\frac{π}{2}$-$\sqrt{2}$
=3$\sqrt{2}$-$\frac{π}{2}$.
故答案为:3$\sqrt{2}$-$\frac{π}{2}$.
点评 本题考查的是扇形面积的计算,根据题意画出图形,利用数形结合求解是解答此题的关键.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
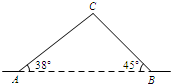 如图,从A地到B地的公路需经过C地,AC=10千米,∠CAB=38°,∠ABC=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.求改直后的公路AB的长(精确到1千米).(参考数据:sin38°=0.62,cos38°=0.79,tan38°=0.78)
如图,从A地到B地的公路需经过C地,AC=10千米,∠CAB=38°,∠ABC=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.求改直后的公路AB的长(精确到1千米).(参考数据:sin38°=0.62,cos38°=0.79,tan38°=0.78)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com