
【题目】某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
乙同学:我发现边数是![]() 时,它也不一定是正多边形,如图
时,它也不一定是正多边形,如图![]() ,
,![]() 是正三角形,
是正三角形,![]() ,证明六边形
,证明六边形![]() 的各内角相等,但它未必是正六边形.
的各内角相等,但它未必是正六边形.
丙同学:我能证明,边数是![]() 时,它是正多边形,我想…,边数是
时,它是正多边形,我想…,边数是![]() 时,它可能也是正多边形.
时,它可能也是正多边形.
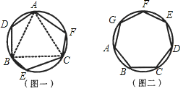
![]() 请你说明乙同学构造的六边形各内角相等;
请你说明乙同学构造的六边形各内角相等;
![]() 请你证明,各内角都相等的圆内接七边形
请你证明,各内角都相等的圆内接七边形![]() (如图
(如图![]() )是正七边形;(不必写已知,求证)
)是正七边形;(不必写已知,求证)
![]() 根据以上探索过程,提出你的猜想.(不必证明)
根据以上探索过程,提出你的猜想.(不必证明)
【答案】![]() 图
图![]() 中六边形各角相等;
中六边形各角相等;![]() 见解析;
见解析;![]() 猜想:当边数是奇数时(或当边数是
猜想:当边数是奇数时(或当边数是![]() ,
,![]() ,
,![]() ,
,![]() ,时),各内角相等的圆内接多边形是正多边形.
,时),各内角相等的圆内接多边形是正多边形.
【解析】
(1)利用等弧对等角证各角相等.(2)利用等弧对等弦证各边相等.(3)根据(1)(2)猜想当边数是奇数时,各内角相等的圆内接多边形是正多边形.
(1)证明:由图知∠AFC对![]() .
.
因为![]() ,∠DAF对的
,∠DAF对的![]() ,
,
所以∠AFC=∠DAF.
因为![]() ,
,![]() ,
,
所以![]() .
.
∠ECF对的![]() ,
,
所以∠AFC=∠ECF.
同理可证∠ADB=∠DBE=∠BEC=∠ECF.
所以图(1)中六边形各角相等.
(2)证明:因为∠A对![]() ,∠B对
,∠B对![]() ,∠A=∠B,
,∠A=∠B,
所以![]() .
.
所以![]() .
.
同理![]() .
.
所以AB=BC=CD=DE=EF=FG=GA.
所以,七边形ABCDEFG是正七边形.
(3)根据(1)(2)可以猜想:当边数是奇数时(或当边数为3,5,7,9,…时),各内角相等的圆内接多边形是正多边形.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“已知底边及底边上的中线作等腰三角形”的尺规作图过程.

已知:如图 1,线段 a 和线段 b.
求作:△ABC,使得 AB = AC,BC = a,BC 边上的中线为 b.
作法:如图 ,
![]()
① 作射线 BM,并在射线 BM 上截取 BC = a;
② 作线段 BC 的垂直平分线 PQ,PQ 交 BC 于 D;
③ 以 D 为圆心,b 为半径作弧,交 PQ 于 A;
④ 连接 AB 和 AC.
则△ABC 为所求作的图形.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图 2 中的图形;
(2)完成下面的证明:
证明:由作图可知 BC = a,AD = b.
∵ PQ 为线段 BC 的垂直平分线,点 A 在 PQ 上,
∴ AB = AC( )(填依据).
又∵线段 BC 的垂直平分线 PQ 交 BC 于 D,
∴ BD=CD.( )(填依据).
∴ AD 为 BC 边上的中线,且 AD = b.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
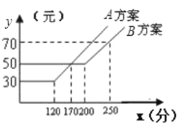
【题目】如图,某电信公司提供了![]() ,
,![]() 两种方案的移动通讯费用
两种方案的移动通讯费用![]() (元)与通话时间
(元)与通话时间![]() (分)之间的关系,则以下说法正确的是( )
(分)之间的关系,则以下说法正确的是( )
①若通话时间少于120分,则![]() 方案比
方案比![]() 方案便宜
方案便宜
②若通话时间超过200分,则![]() 方案比
方案比![]() 方案便宜
方案便宜
③通讯费用为60元,则![]() 方案比
方案比![]() 方案的通话时间多
方案的通话时间多
④当通话时间是170分钟/时,两种方案通讯费用相等
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班为了配合学校体育文化月活动的开展,同学们从捐助的班费中拿出一部分钱来购买羽毛球拍和跳绳。已知购买一副羽毛球拍比购买一根跳绳多20元。若用200元购买羽毛球拍和用80元购买跳绳,则购买羽毛球拍的副数是购买跳绳根数的一半。
(1)求购买一副羽毛球拍、一根跳绳各需多少元?
(2)双11期间,商店老板给予优惠,购买一副羽毛球拍赠送一根跳绳,如果八(1)班需要的跳绳根数比羽毛球拍的副数的![]() 倍还多
倍还多![]() ,且该班购买羽毛球拍和跳绳的总费用不超过
,且该班购买羽毛球拍和跳绳的总费用不超过![]() 元,那么八(1)班最多可购买多少副羽毛球拍?
元,那么八(1)班最多可购买多少副羽毛球拍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=(x-2)2+m与x轴交于点A和B,与y轴交于点C,点D是点C关于抛物线对称轴的对称点,若点A的坐标为(1,0),直线y2=kx+b经过点A,D.
(1)求抛物线的函数解析式;
(2)求点D的坐标和直线AD的函数解析式;
(3)根据图象指出,当x取何值时,y2>y1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=2x2﹣8x+m满足以下条件:当﹣2<x<﹣1时,它的图象位于x轴的下方;当6<x<7时,它的图象位于x轴的上方,则m的值为( )
A. 8 B. ﹣10 C. ﹣42 D. ﹣24
查看答案和解析>>
科目:初中数学 来源: 题型:
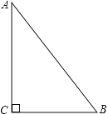
【题目】如图,△ABC中,∠C=90°,AC=4cm,BC=3cm,若动点P从点C开始,沿C→A→B→C的路径运动一周,且速度为每秒2cm,设运动时间为t秒,当t=_____时,点P与△ABC的某两个顶点构成等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“感冒”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后y与x成反比例如图。现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中提供的信息,解答下列问题:
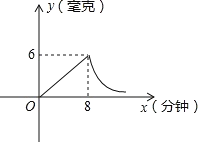
(1)药物燃烧时,y关于x的函数关系式为___,自变量x的取值范围是___;药物燃烧后y关于x的函数关系式为___.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过___分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病毒,那么此次消毒有效吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com