
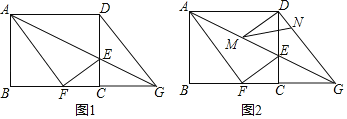
【题目】如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G.
(1)求线段CE的长;
(2)如图2,M,N分别是线段AG,DG上的动点(与端点不重合),且∠DMN=∠DAM,设AM=x,DN=y.
①写出y关于x的函数解析式,并求出y的最小值;
②是否存在这样的点M,使△DMN是等腰三角形?若存在,请求出x的值;若不存在,请说明理由.
【答案】(1)3;(2)①y=![]() x2﹣
x2﹣![]() x+10,y有最小值为2;②存在,8
x+10,y有最小值为2;②存在,8![]() ﹣10或
﹣10或![]() .
.
【解析】
(1)由翻折可知:AD=AF=10,DE=EF,求出BF,设EC=x,则DE=EF=8﹣x,在Rt△ECF中,利用勾股定理构建方程即可解决问题;
(2)①首先求出AG,DG,∠ADM=∠NMG,证明△ADM∽△GMN,可得![]() ,整理后根据二次函数的最值求解即可.
,整理后根据二次函数的最值求解即可.
②存在.有两种情形:如图3﹣1中,当MN=MD时.如图3﹣2中,当MN=DN时,分别通过证明三角形相似,利用相似三角形的性质求解即可.
解:(1)如图1中,
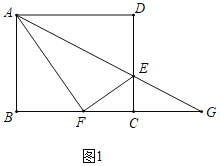
∵四边形ABCD是矩形,
∴AD=BC=10,AB=CD=8,∠B=∠BCD=90°,
由翻折可知:AD=AF=10,DE=EF,
在Rt△ABF中,BF=![]() =6,
=6,
∴CF=BC﹣BF=10﹣6=4,
设CE=x,则DE=EF=8﹣x,
在Rt△EFC中,则有:(8﹣x)2=x2+42,
∴x=3,即CE=3.
(2)①如图2中,
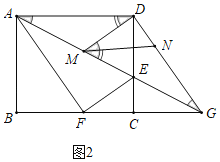 ,
,
∵AD∥CG,
∴![]() ,
,
∴![]() ,
,
∴CG=6,
∴BG=BC+CG=16,
在Rt△ABG中,AG=![]() ,
,
在Rt△DCG中,DG=![]() ,
,
∵AD=DG=10,
∴∠DAG=∠AGD,
∵∠DMG=∠DMN+∠NMG=∠DAM+∠ADM,∠DMN=∠DAM,
∴∠ADM=∠NMG,
∴△ADM∽△GMN,
∴![]() ,
,
∴![]() ,
,
∴y=![]() x2﹣
x2﹣![]() x+10,
x+10,
∴当x=4![]() 时,y有最小值,将x=4
时,y有最小值,将x=4![]() 代入可得,最小值=2;
代入可得,最小值=2;
②存在,
由①可得∠DMN=∠DGM,
∴∠DNM=∠DMG,
∴∠DNM≠∠DMN,
所以有两种情形:如图3﹣1中,当MN=MD时,
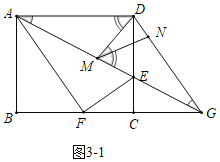
∵∠MDN=∠GDM,∠DMN=∠DGM,
∴△DMN∽△DGM,
∴![]() ,
,
∵MN=DM,
∴DG=GM=10,
∴x=AM=8![]() ﹣10.
﹣10.
如图3﹣2中,当MN=DN时,作MH⊥DG于H.
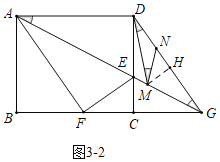
∵MN=DN,
∴∠MDN=∠DMN,
∵∠DMN=∠DGM,
∴∠MDG=∠MGD,
∴MD=MG,
∵MH⊥DG,
∴DH=GH=5,
∵∠DAG=∠DGA,∠DAG=∠AGB,
∴∠DGA=∠AGB,
又∵∠MHG=∠ABG=90°,
∴△GHM∽△GBA,
∴![]() ,
,
∴![]() ,
,
∴MG=![]() ,
,
∴x=AM=8![]() ﹣
﹣![]() =
=![]() .
.
综上所述,满足条件的x的值为8![]() ﹣10或
﹣10或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】改革开放40年来,中国已经成为领先世界的基建强国,如图①是建筑工地常见的塔吊,其主体部分的平面示意图如图②,点F在线段HG上运动,BC∥HG,AE⊥BC,垂足为点E,AE的延长线交HG于点G,经测量,∠ABD=11°,∠ADE=26°,∠ACE=31°,BC=20m,EG=0.6m.
(1)求线段AG的长度;
(2)连接AF,当线段AF⊥AC时,求点F和点G之间的距离.
(所有结果精确到0.1m.参考数据:tan11°≈0.19,tan26°≈0.49,tan31°≈0.60)
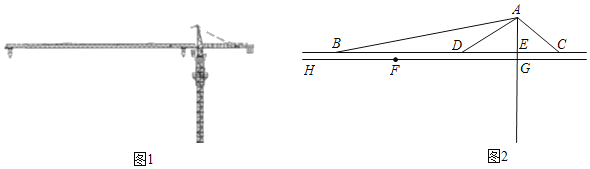
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物BC的高度,他们先在斜坡上的D处,测得建筑物顶端B的仰角为30°.且D离地面的高度DE=5m.坡底EA=30m,然后在A处测得建筑物顶端B的仰角是60°,点E,A,C在同一水平线上,求建筑物BC的高.(结果用含有根号的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批进价为20元/件的日用商品,第一个月,按进价提高50%的价格出售,售出400件;第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量y(件)与销售单价x(元)的关系如图所示.
(1)求y与x之间的函数表达式;
(2)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=2x+8的图象分别交x轴、y轴于A、B两点,过点A的直线交y轴正半轴于点M,且点M为线段OB的中点.

(1)求直线AM的函数解析式.
(2)试在直线AM上找一点P,使得S△ABP=S△AOB,求出点P的坐标.
(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、B、M、H为顶点的四边形是平行四边形?若存在,请直接写出所有点H的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至27日在湖北武汉举行,这是中国首次承办世界军人运动会.现有两张纪念卡片分别绘有会徽和吉祥物的图案(如下图),纪念卡背面完全相同.

(1)小丽从两张纪念卡任意摸一张,则小丽摸到绘有吉祥物“兵兵”的概率为______;
(2)如果小丽摸两次(第一次摸出后记录并放回),求小丽两次摸到的纪念卡相同的概率.(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
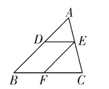
【题目】如图,在△ABC 中,D、E、F 分别为边 AB、AC、BC 上的点,连接 DE、EF.若 DE∥BC,EF∥AB,则图中共有________对相似三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com