
【题目】用反证法证明:在△ABC中,如果M、N分别是边AB、AC上的点,那么BN、CM不能互相平分.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
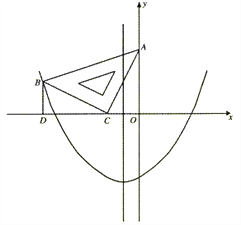
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C为 (-1,0) .如图所示,B点在抛物线y=![]() x2+
x2+![]() x-2图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
x-2图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
(1)求证:△BDC≌△COA;
(2)求BC所在直线的函数关系式;
(3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆轿车从甲地出发开往乙地,同时,一辆客车从乙地开往甲地,一开始两车的速度相同,出发半小时后,客车因出现故障维修了一段时间,修好后为了不耽误乘客的时间,客车加快速度前进,结果与轿车同时到达各自的目的地.设轿车出发th后,与客车的距离为Skm,图中的折线(A→B→C→D→E)表示S与t之间的函数关系.
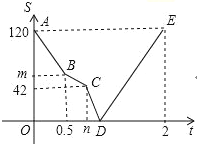
(1)甲、乙两地相距 km,轿车的速度为 km/h;
(2)求m与n的值;
(3)求客车修好后行驶的速度;
(4)求线段DE所对应的函数关系式,并注明自变量的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com