
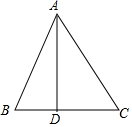
 如图,在△ABC中,AB=26,BC=28,AC=30,求BC边上的高AD.
如图,在△ABC中,AB=26,BC=28,AC=30,求BC边上的高AD.  小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )| A. | 大于90° | B. | 等于90° | C. | 小于90° | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线AC∥BD,P在直线AB上(不与点A,B重合).
如图,直线AC∥BD,P在直线AB上(不与点A,B重合).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
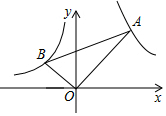 如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{2}{x}$,y=$\frac{8}{x}$的图象交于B、A两点,则tan∠OAB的值的变化趋势为:( )
如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{2}{x}$,y=$\frac{8}{x}$的图象交于B、A两点,则tan∠OAB的值的变化趋势为:( )| A. | 逐渐变小 | B. | 逐渐变大 | C. | 时大时小 | D. | 保持不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )| A. | AB∥DC | B. | AC=BD | C. | AC⊥BD | D. | OA=OC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
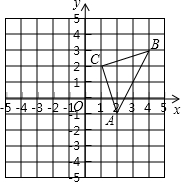 如图所示,△ABC的顶点都在平面直角坐标系的网格上.
如图所示,△ABC的顶点都在平面直角坐标系的网格上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.4×1013元 | B. | 240000×108元 | C. | 24×1012元 | D. | 24×108元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
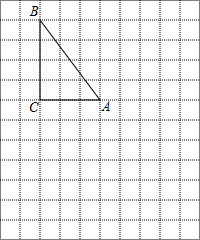 在右边网格图中,每个小正方形的边长均为1个单位长度,△ABC为直角三角形,∠C=90°,AC=3,BC=4.
在右边网格图中,每个小正方形的边长均为1个单位长度,△ABC为直角三角形,∠C=90°,AC=3,BC=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com