
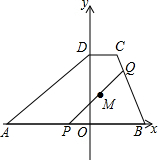
 ��ͼ����ƽ��ֱ������ϵ�У��ı���ABCD�Ķ���A��B��x���ϣ���D��y���ϣ�AB��CD��ֱ��BC����ʽΪy=-$\frac{4}{3}$x+16����A��D������ֱ�Ϊ��-16��0������0��12��������P�ӵ�A������AB������Q�ӵ�B�������ı���ABCD��BC-CD-DA����ͬʱ��ʼ�˶����ٶȾ�Ϊÿ��1����λ����P�㵽��B��ʱ��������ͬʱֹͣ�˶������˶�ʱ��Ϊt��
��ͼ����ƽ��ֱ������ϵ�У��ı���ABCD�Ķ���A��B��x���ϣ���D��y���ϣ�AB��CD��ֱ��BC����ʽΪy=-$\frac{4}{3}$x+16����A��D������ֱ�Ϊ��-16��0������0��12��������P�ӵ�A������AB������Q�ӵ�B�������ı���ABCD��BC-CD-DA����ͬʱ��ʼ�˶����ٶȾ�Ϊÿ��1����λ����P�㵽��B��ʱ��������ͬʱֹͣ�˶������˶�ʱ��Ϊt������ ��1����ֱ��BC����ʽΪy=-$\frac{4}{3}$x+16����y=0ʱ��0=-$\frac{4}{3}$x+16�����x=12���ɵ�B��12��0������y=12ʱ��12=-$\frac{4}{3}$x+16�����x=3���ɵ�C��3��12�����õ�P�����꣨-16+t��0����Q�����꣨12-0.6t��0.8t����ֱ��б��Ϊ-$\frac{4}{3}$���˶��ٶ�Ϊ1����Q��x�᷽�������ƶ�0.6�������ƶ�0.8�������е����깫ʽ��M�����ꣻ
�ڼ�M��x0��y0����x0=2+0.2t��y0=0.4t���õ�y0=2x0+4���Ӷ��õ���M��ijһ�κ���y=2x+4�ϣ�
��k1=$\frac{1.6t-28}{0.8t}$��l����M��-2+0.2t��0.4t�����õ�бʽ��$\frac{y-0.4t}{x+2-0.2t}$=$\frac{1.6t-28}{0.8t}$���õ�y=$\frac{2t-35}{t}$x+11-$\frac{70}{t}$��
��x=-2ʱ��y=7���ɵ�l�����㣨-2��7����
��2��������������ٵ�PQ��ABʱ����BC��PQ��0��t��15��ʱ����PQ��CD��15��t��18��ʱ����PQ��DA��18��t��28��ʱ���������ۿ���t��ֵ��
��� �⣺��1���١�ֱ��BC����ʽΪy=-$\frac{4}{3}$x+16��
��y=0ʱ��0=-$\frac{4}{3}$x+16�����x=12��
��B��12��0����
��y=12ʱ��12=-$\frac{4}{3}$x+16�����x=3��
��C��3��12����
�ߵ�A��D������ֱ�Ϊ��-16��0������0��12����AB��BC��
��P�����꣨-16+t��0����Q�����꣨12-0.6t��0.8t����ֱ��б��Ϊ-$\frac{4}{3}$���˶��ٶ�Ϊ1����Q��x�᷽�������ƶ�0.6�������ƶ�0.8����
�����е����깫ʽ��M��-2+0.2t��0.4t����
���ǣ���M��x0��y0����x0=2+0.2t��y0=0.4t��
��y0=2x0+4��
���M��ijһ�κ���y=2x+4�ϣ�
��k1=$\frac{1.6t-28}{0.8t}$��l����M��-2+0.2t��0.4t�����õ�бʽ��$\frac{y-0.4t}{x+2-0.2t}$=$\frac{1.6t-28}{0.8t}$��
������-0.8ty=��28-1.6t��x+56-8.8t��
y=$\frac{2t-35}{t}$x+11-$\frac{70}{t}$��
x=-2ʱ��y=7��
��l�����㣨-2��7����
��2��P�����꣨-16+t��0����0��t��28��
Q�����꣨12-0.6t��0.8t����0��t��15������18-t��12����15��t��18������14.4-0.8t��-0.6t+2����18��t��28����
�ٵ�PQ��ABʱ��P��Q��������ȣ�t=17��
��BC��PQ��0��t��15��ʱ��kPQ=$\frac{3}{4}$�����t=10.5��
��PQ��CD��15��t��18��ʱ��P��Q��������ȣ�t=17����ظ���
��PQ��DA��18��t��28��ʱ��kQP=-$\frac{4}{3}$��t=19��
����������tΪ10.5��17��19ʱ����PQΪֱ����Բ�������ı���ABCD����һ�㣮
���� ������һ�κ����ۺ��⣬�漰��֪ʶ���У�ֱ��б�ʣ��е����깫ʽ������˼�룬����˼���Ӧ�ã��ۺ��Խ�ǿ����һ�����Ѷȣ�


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
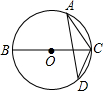 ��ͼ��A��D�ǡ�O�ϵ������㣬BC��ֱ��������D=35�㣬���ACB�Ķ����ǣ�������
��ͼ��A��D�ǡ�O�ϵ������㣬BC��ֱ��������D=35�㣬���ACB�Ķ����ǣ�������| A�� | 35�� | B�� | 55�� | C�� | 65�� | D�� | 70�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������� | |
| B�� | Сǿ��ĩ��ѧ���Ի��100�� | |
| C�� | ���ڶ������ѩ | |
| D�� | ��һ��ֻװ��10������Ĵ�������������һ���պ��Ǻ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
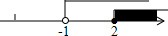 ��⼯����������ʾ�IJ���ʽ��Ϊ��������
��⼯����������ʾ�IJ���ʽ��Ϊ��������| A�� | $\left\{\begin{array}{l}{x+1��0}\\{x-2��0}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x+1��0}\\{x-2��0}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x+1��0}\\{2-x��0}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x+1��0}\\{2-x��0}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com