
【题目】已知△ABC的外角∠CBE,∠BCF的角平分线BP,CP交于P点,则∠BPC是( )
A.钝角
B.锐角
C.直角
D.无法确定
【答案】B
【解析】解: 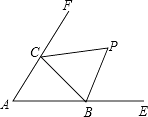
∵△ABC的外角平分线BP,CP交于P点,
∴∠PBC= ![]() ∠EBC,∠BCP=
∠EBC,∠BCP= ![]() ∠BCF,
∠BCF,
∵∠CBE、∠BCF是△ABC的两个外角,
∴∠CBE+∠BCF=360°﹣(180°﹣∠A)=180°+∠A,
∴∠PBC+∠BCP= ![]() (∠EBC+∠BCF)=
(∠EBC+∠BCF)= ![]() (180°+∠A)=90°+
(180°+∠A)=90°+ ![]() ∠A,
∠A,
∵在△PBC中,∠BPC=180°﹣(∠PBC+∠BCP)=180°﹣(90°+ ![]() ∠A)=90°﹣
∠A)=90°﹣ ![]() ∠A<90°,
∠A<90°,
∴∠BPC是锐角.
故选:B.
首先根据△ABC的外角平分线BP,CP交于P点,得出∠PBC+∠BCP=90°+ ![]() ∠A,再根据三角形内角和定理,求得∠BPC=90°﹣
∠A,再根据三角形内角和定理,求得∠BPC=90°﹣ ![]() ∠A<90°即可.
∠A<90°即可.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2 , 且l4和l1、l2分别交于A、B两点,点P为线段AB上的一个定点如图1) 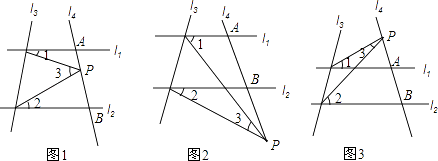
(1)写出∠1、∠2、∠3、之间的关系并说出理由.
(2)如果点P为线段AB上的动点时,问∠1、∠2、∠3之间的关系是否发生变化?(必说理由)
(3)如果点P在A、B两点外侧运动时,(点P和点A、点B不重合)
①如图2,当点P在射线AB上运动时,∠1、∠2、∠3之间关系并说出理由.
②如图3,当点P在射线BA上运动时,∠1、∠2、∠3之间关系(不说理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2.说明:∠DGA+∠BAC=180°.请将说明过程填写完成.
解:∵EF∥AD,(已知)
∴∠2= . ()
又∵∠1=∠2,()
∴∠1=∠3,()
∴AB∥ , ()
∴∠DGA+∠BAC=180°.()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com