
【题目】如图所示,在平面直角坐标系中,一次函数y=kx+1的图象与反比例函数y=![]() 的图象在第一象限相交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C,如果四边形OBAC是正方形.
的图象在第一象限相交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C,如果四边形OBAC是正方形.
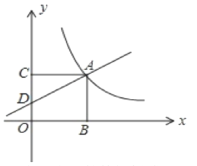
(1)求一次函数的解析式。
(2)一次函数的图象与y轴交于点D. 在x轴上是否存在一点P,使得PA+PD最小?若存在,请求出P点坐标及最小值;若不存在,请说明理由。
【答案】(1)y=![]() x+1;(2)(
x+1;(2)(![]() ,0)
,0)
【解析】
(1)若四边形OBAC是正方形,那么点A的横纵坐标相等,代入反比例函数即可求得点A的坐标,进而代入一次函数即可求得未知字母k.
(2)在y轴负半轴作OD′=OD,连接AD′,与x轴的交点即为P点的坐标,进而求出P点的坐标.
(1)∵四边形OBAC是正方形,
∴S四边形OBAC=AB![]() =OB
=OB![]() =9,
=9,
∴点A的坐标为(3,3),
∵一次函数y=kx+1的图象经过A点,
∴3=3k+1,
解得k=![]() ,
,
∴一次函数的解析式y=![]() x+1,
x+1,
(2)y轴负半轴作OD′=OD,连接AD′,如图所示,AD′与x轴的交点即为P点的坐标,
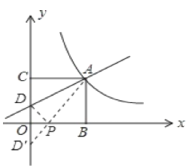
∵一次函数的解析式y=![]() x+1,
x+1,
∴D点的坐标为(0,1),
∴D′的坐标为(0,1),
∵A点坐标为(3,3),
设直线AD′的直线方程为y=mx+b,
即![]() ,
,
解得m=![]() ,b=1,
,b=1,
∴直线AD′的直线方程为y=![]() x1,
x1,
令y=0,解得x=![]() ,
,
∴P点坐标为(![]() ,0)
,0)


科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.

【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵![]()
∴![]()
∴![]()

点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.
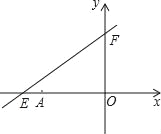
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”国际合作高峰论坛期间,我国同30多个国家签署经贸合作协议.某工厂准备生产甲、乙两种商品共6万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于4200万元,则至少销管甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个.设每个定价增加x元.
(1)写出售出一个可获得的利润是多少元(用含x的代数式表示)?
(2)商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?应进货多少个?
(3)商店若要获得最大利润,则每个应定价多少元?获得的最大利润是多少?
【答案】(1)x+10元;(2)每个定价为70元,应进货200个.(3)每个定价为65元时得最大利润,可获得的最大利润是6250元.
【解析】试题分析:(1)根据利润=销售价-进价列关系式,(2)总利润=每个的利润×销售量,销售量为400-10x,列方程求解,根据题意取舍,(3)利用函数的性质求最值.
试题解析:由题意得:(1)50+x-40=x+10(元),
(2)设每个定价增加x元,
列出方程为:(x+10)(400-10x)=6000,解得:x1=10,x2=20,要使进货量较少,则每个定价为70元,应进货200个,
(3)设每个定价增加x元,获得利润为y元,
y=(x+10)(400-10x)=-10x2+300x+4000=-10(x-15)2+6250,当x=15时,y有最大值为6250,所以每个定价为65元时得最大利润,可获得的最大利润是6250元.
【题型】解答题
【结束】
24
【题目】猜想与证明:
如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.
拓展与延伸:
(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为 .
(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)5![]() ﹣(﹣2
﹣(﹣2![]() )+(﹣3
)+(﹣3![]() )﹣(+4
)﹣(+4![]() )
)
(2)(﹣![]() ﹣
﹣![]() +
+![]() )×(﹣24)
)×(﹣24)
(3)(﹣3)÷![]() ×
×![]() ×(﹣15)
×(﹣15)
(4)﹣14+|(﹣2)3﹣10|﹣(﹣3)÷(﹣1)2017.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市提倡“诵读中华经典,营造书香校园”的良好诵读氛围,促进校园文化建设,进而培养学生的良好诵读习惯,使经典之风浸漫校园.某中学为了了解学生每周在校经典诵读时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
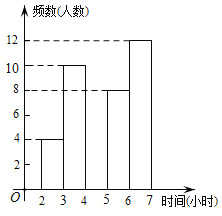
(3)若该校共有1200名学生,试估计全校每周在校参加经典诵读时间至少有4小时的学生约为多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com