
【题目】甲乙两个工程队承包了地铁某标段全长3900米的施工任务,分别从南,北两个方向同时向前掘进。已知甲工程队比乙工程队平均每天多掘进0.4米经过13天的施工两个工程队共掘进了156米.
(1)求甲,乙两个工程队平均每天各掘进多少米?
(2)为加快工程进度两工程队都改进了施工技术,在剩余的工程中,甲工程队平均每天能比原来多掘进0.4米,乙工程队平均每天能比原来多掘进0.6米,按此施工进度能够比原来少用多少天完成任务呢?
【答案】(1)甲工程队平均每天掘进6.2米,乙工程队平均每天掘进5.8米;(2)24天.
【解析】
(1)设甲工程队平均每天掘进![]() 米,则乙工程队平均每天掘进
米,则乙工程队平均每天掘进![]() 米,根据“经过13天的施工两个工程队共掘进了156米”列出等式方程,求解即可得;
米,根据“经过13天的施工两个工程队共掘进了156米”列出等式方程,求解即可得;
(2)先根据题(1)计算出来的甲乙两个工程队的掘进速度,计算在剩余的工程中所需花费的时间;再根据调整后的掘进速度,计算在剩余的工程中所需花费的时间,两者之差即为所求.
(1)设甲工程队平均每天掘进![]() 米,则乙工程队平均每天掘进
米,则乙工程队平均每天掘进![]() 米
米
由题意得:![]()
解得:![]()
则乙工程队平均每天掘进的距离为:![]() (米)
(米)
答:甲工程队平均每天掘进6.2米,乙工程队平均每天掘进5.8米;
(2)由题(1)得,在剩余的工程中,甲乙两个工程队所需时间为:![]() (天)
(天)
在改进施工技术后,甲工程队平均每天可掘进的距离为:![]() (米);乙工程队平均每天可掘进的距离为:
(米);乙工程队平均每天可掘进的距离为:![]() (米)
(米)
则此时在剩余的工程中,甲乙两个工程队所需时间为:![]() (天)
(天)
故按此施工进度能够比原来少用时间为:![]() (天)
(天)
答:在改进施工技术后,甲乙两个工程队完成任务的时间比原来要少用24天.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图:在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF。
⑴△BCE与△DCF全等吗?说明理由;
⑵若∠BEC=60o,求∠EFD。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.
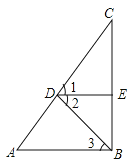
证明:∵ DE⊥BC,AB⊥BC(已知)
∴∠DEC=∠ABC=90°( )
∴DE∥AB(_________ ___)
∴∠2=____ (__________ ___________)
∠1= (____________ _________)
又∵∠1=∠2(_____________________)
∴∠A=∠3(_____________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
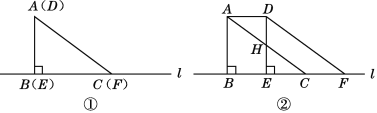
【题目】两个全等的直角三角形重叠放在直线l上,如图①所示,AB=6 cm,AC=10 cm,∠ABC=90°,将Rt△ABC在直线l上左右平移(如图②).
(1)求证:四边形ACFD是平行四边形.
(2)怎样移动Rt△ABC,使得四边形ACFD的面积等于△ABC的面积的一半?
(3)将Rt△ABC向左平移4 cm,求四边形DHCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
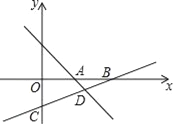
【题目】如图,直线l1:y=﹣x+3与x轴相交于点A,直线l2:y=kx+b经过点(3,﹣1),与x轴交于点B(6,0),与y轴交于点C,与直线l1相交于点D.
(1)求直线l2的函数关系式;
(2)点P是l2上的一点,若△ABP的面积等于△ABD的面积的2倍,求点P的坐标;
(3)设点Q的坐标为(m,3),是否存在m的值使得QA+QB最小?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是一块含有45的直角三角板,四边形DEFG是长方形,D、G分别在AB、AC上,E、F在BC上。BC=16,DG=4,DE=6,现将长方形 DEFG向右沿BC方向平移,设水平移动的距离为d,长方形与直角三角板的重叠面积为S,
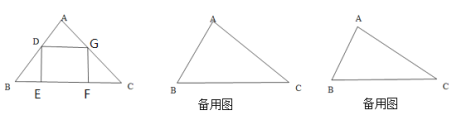
(1)当水平距离d是何值时,长方形 DEFG恰好完全移出三角板;
(2)在移动过程中,请你用含有d的代数式表示重叠面积S,并写出相应的d的范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.  B.
B. 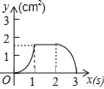 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计307元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售.
(1)若存放x天后,将这批野生菌一次性出售,设这批野生菌的销售总额为P元,试写出P与x之间的函数关系式,并写出自变量x的取值范围.
(2)李经理将这批野生茵存放多少天后出售可获得最大利润W元?(利润=销售总额﹣收购成本﹣各种费用)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com