
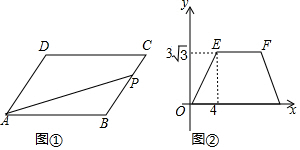
| A. | 7 | B. | 8 | C. | 4+2$\sqrt{3}$ | D. | 4+$\sqrt{3}$ |
分析 作CM⊥AB于M,根据三角形面积公式可得当点P在CD上运动时,△PAB的面积不变,再联系函数图象可得BC=cm,则AB=3cm,然后根据三角函数求出CM,三角形面积公式求出AB,即可得出结果.
解答 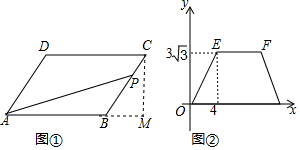 解:作CM⊥AB于M如图所示:
解:作CM⊥AB于M如图所示:
当点P在CD上运动时,△PAB的面积不变,
由图②得:BC=4cm,
∵∠ABC=120°,
∴∠CBM=60°,
∴CM=BC•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∵△ABC的面积=$\frac{1}{2}$AB•CM=$\frac{1}{2}$AB×2$\sqrt{3}$=3$\sqrt{3}$,
∴AB=3cm,
∴点F的横坐标为4+3=7.
故选:A.
点评 本题考查了平行四边形的性质、动点问题的函数图象.解决本题的关键是利用函数图象和三角形面积确定AB的长.


科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,E是边BC的一点,F是边CD的中点,CE=k•BE,且四边形AECF的面积为2.
如图,矩形ABCD中,E是边BC的一点,F是边CD的中点,CE=k•BE,且四边形AECF的面积为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
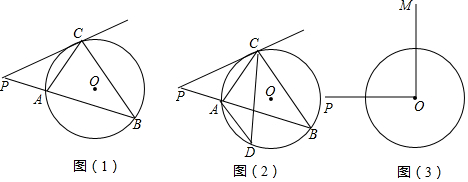
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
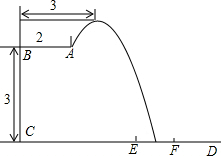 2016年里约奥运会,中国跳水队赢得8个项目中的7块金牌,优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.
2016年里约奥运会,中国跳水队赢得8个项目中的7块金牌,优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
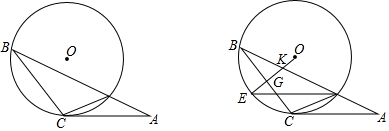
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
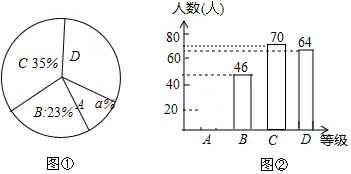
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com