
分析 (1)设三个水管同时开放x小时可注满水池,根据“甲、乙注水量-丙出水量=1”列出方程并解答;
(2)设共需y小时可注满水池,根据“甲、乙注水量-丙出水量=1”列出方程并解答;
(3)设开放甲管1小时后后关闭,再开放乙、丙两管,需z小时可注满水池,根据“甲、乙注水量-丙出水量=1”列出方程并解答.
解答 解:(1)设三个水管同时开放x小时可注满水池,根据题意得
($\frac{1}{3}$+$\frac{1}{6}$)x-$\frac{x}{4}$=1,
解得x=4,
所以三个水管同时开放4小时可注满水池;
(2)设共需y小时可注满水池,依题意得
$\frac{y}{3}$+$\frac{y-1}{6}$-$\frac{y-1}{4}$=1,
解得y=$\frac{11}{3}$,
所以若甲管先开放1小时,而后同时开放乙、丙两个水管,则共需$\frac{11}{3}$小时可注满水池;
(3)设开放甲管1小时后后关闭,再开放乙、丙两管,需z小时可注满水池,根据题意得
$\frac{1}{3}$+$\frac{z}{6}$-$\frac{z}{4}$=1
解得z=-8,
因为-8<0不符合实际意义,
所以先甲管1小时后,再开放乙、丙两管不能注满水池.
点评 本题考查了一元一次方程的应用.关于工程问题,需要用到的等量关系是:工作效率=工作量÷工作时间.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
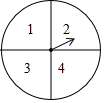 元旦期间,某商场设置了如图所示的幸运转盘,转盘分成4个大小相同的扇形,分别标有数学1,2,3,4,指针的位置固定,转盘可以自由转动,当转动的转盘停止后,其中的某个扇形会停在指针所指的位置(指针指向两个扇形的交线时,当作右边的扇形).商场规定:凡是参加抽奖的顾客均可转动转盘两次,如果两次转动中指针指缶扇形上的数字之和为8是一等奖,数字之和为7是二等奖,数字之和为6是三等奖,标号之和为其他数字则获得一份纪念品,请分别求出顾客抽中一、二、三等奖的概率.
元旦期间,某商场设置了如图所示的幸运转盘,转盘分成4个大小相同的扇形,分别标有数学1,2,3,4,指针的位置固定,转盘可以自由转动,当转动的转盘停止后,其中的某个扇形会停在指针所指的位置(指针指向两个扇形的交线时,当作右边的扇形).商场规定:凡是参加抽奖的顾客均可转动转盘两次,如果两次转动中指针指缶扇形上的数字之和为8是一等奖,数字之和为7是二等奖,数字之和为6是三等奖,标号之和为其他数字则获得一份纪念品,请分别求出顾客抽中一、二、三等奖的概率.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com