
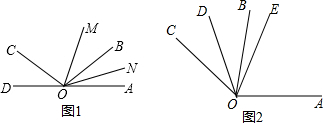
分析 (1)由角平分线定义和补角定义得出方程,解方程即可得出结果;
(2)设∠AOB=3x,∠BOC=2x.则∠AOC=∠AOB+∠BOC=5x.由角平分线定义和已知条件求出x=24°,即可得出所求角的度数.
解答 解:(1)设∠AOB=x,因为∠AOC与∠AOB互补,则∠AOC=180°-x.
由题意,得$\frac{1}{2}$(180°-x)-$\frac{1}{2}$x=40°.
解得:x=50°,
∴∠AOB=50°,∠AOC=130°.
(2)解:设∠AOB=3x,∠BOC=2x.
则∠AOC=∠AOB+∠BOC=5x.
∵OE是∠AOC的平分线,
∴∠AOE═$\frac{1}{2}∠AOC=\frac{5}{2}x$,
∴∠BOE=∠AOB-∠AOE=$3x-\frac{5}{2}x=\frac{1}{2}x$,
∵∠BOE=12°,
∴$\frac{1}{2}x=12°$,
解得:x=24°,
∵OD是∠BOC的平分线,
∴$∠BOD=\frac{1}{2}∠BOC=x=24°$,
∴∠DOE=∠DOB+∠BOE=24°+12°=36°.
点评 此题考查了补角的定义、角平分线的定义及角的运算.熟练掌握补角定义和角平分线定义,根据题意得出方程是解决问题的关键.


科目:初中数学 来源: 题型:填空题
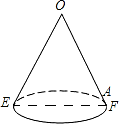 如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,则圆锥的侧面积是50π,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.
如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,则圆锥的侧面积是50π,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m,则A,B两点间的距离是( )
如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m,则A,B两点间的距离是( )| A. | 200m | B. | 20$\sqrt{10}$m | C. | 40$\sqrt{2}$m | D. | 50m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | sinA=$\frac{5}{13}$ | B. | cosA=$\frac{12}{13}$ | C. | tanA=$\frac{13}{12}$ | D. | $\frac{1}{tanA}$=$\frac{5}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “+15米”表示向东走15米 | |
| B. | 0℃表示没有温度 | |
| C. | 在一个正数前添上一个负号,它就成了负数 | |
| D. | 0 既是正数也是负数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com