
 如图,已知OA=OB.
如图,已知OA=OB.科目:初中数学 来源: 题型:解答题
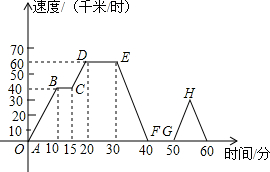 星期天到外婆家去,他记录了汽车行驶的速度随时间的变化情况,到了外婆家画出如图所示的图象
星期天到外婆家去,他记录了汽车行驶的速度随时间的变化情况,到了外婆家画出如图所示的图象查看答案和解析>>
科目:初中数学 来源: 题型:解答题
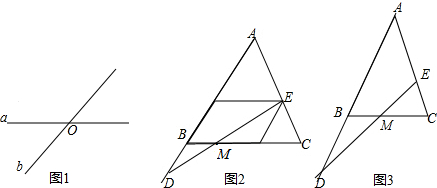
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:$\sqrt{12}+(-\frac{1}{2})^{-1}$-2tan60°-(-1)2015;
(1)计算:$\sqrt{12}+(-\frac{1}{2})^{-1}$-2tan60°-(-1)2015;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
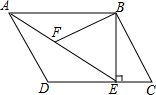 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.下列结论:
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.下列结论:| A. | ①②③④ | B. | ②③ | C. | ②④ | D. | ③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com