
【题目】已知一次函数y=﹣ ![]() x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.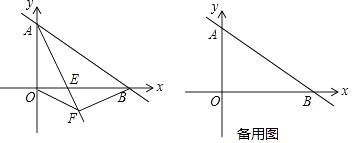
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
【答案】
(1)解:当y=﹣ ![]() x+6=0时,x=8,
x+6=0时,x=8,
∴点B的坐标为(8,0).
(2)解:当x=0时,y=﹣ ![]() x+6=6,
x+6=6,
∴点A的坐标为(0,6),
∴OA=6,OB=8,
∴AB= ![]() =10.
=10.
∵AE平分∠BAO,交x轴于点E,
∴ ![]() =
= ![]() ,
,
∴OE= ![]() BE.
BE.
∵OE+BE=OB=8,
∴OE=3,BE=5,
∴点E的坐标为(3,0).
设直线AE的表达式为y=kx+b,
将A(0,6)、E(3,0)代入y=kx+b,
![]() ,解得:
,解得: ![]() ,
,
∴直线AE的表达式为y=﹣2x+6.
(3)解:过点F作FG⊥x轴于点G,如图所示.
∵BF⊥AE,
∴∠BFE=90°=∠AOE.
∵∠AEO=∠BEF,
∴△AOE∽△BFE,
∴ ![]() =
= ![]() =
= ![]() .
.
∵OA=6,OE=3,
∴AE=3 ![]() .
.
∵BE=5,
∴BF=2 ![]() ,EF=
,EF= ![]() .
.
同理可得:△BEF∽△BFG,
∴BG=4,FG=2.
∵OB=8,
∴OG=4=BG,
∴△OFB为等腰三角形,
∴S△OFB= ![]() OBFG=8.
OBFG=8.
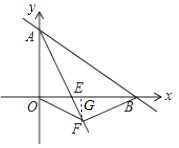
【解析】(1)将y=0代入直线AB的表达式中求出x值,此题得解;(2)利用一次函数图象上点的坐标特征求出点A的坐标,结合勾股定理可求出AB的长度,再利用角平分线的性质即可求出点E的坐标,根据点A、E的坐标利用待定系数法即可求出直线AE的表达式;(3)过点F作FG⊥x轴于点G,由BF⊥AE可得出△AOE∽△BFE,根据相似三角形的性质可得出BF、EF的长度,同理可得出△BEF∽△BFG,根据相似三角形的性质可得出BG、FG的长度,结合OB=8即可得出OG=BG,由此可得出△OFB为等腰三角形,再根据三角形的面积公式可得出△OFB的面积.
【考点精析】掌握相似三角形的性质是解答本题的根本,需要知道对应角相等,对应边成比例的两个三角形叫做相似三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),那么A2020坐标为( )

A.(2020,1)B.(2020,0)C.(1010,1)D.(1010,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:
成绩 | 频数 | 频率 |
优秀 | 45 | b |
良好 | a | 0.3 |
合格 | 105 | 0.35 |
不合格 | 60 | c |

(1)该校初四学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初四(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2017年“KFC”乒乓球赛进校园活动中,某校甲、乙两队进行决赛,比赛规则规定:两队之间进行3局比赛,3局比赛必须全部打完,只要赢2局的队为获胜队,假如甲、乙两队之间每局比赛输赢的机会相同,且乙队已经赢得了第1局比赛.
(1)列表或画树状图表示乙队所有比赛结果的可能性;
(2)求乙队获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题: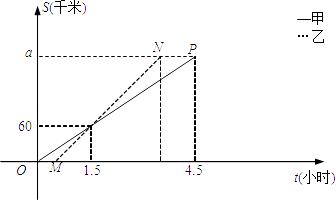
(1)计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回.
①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;
②请问甲车在离B地多远处与返程中的乙车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,求证:BE2+CF2=EF2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com