
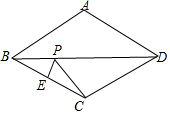
 如图,在菱形ABCD中,∠ABC=60°,AB=1,E为BC的中点,则对角线BD上的动点P到E、C两点的距离之和的最小值为( )
如图,在菱形ABCD中,∠ABC=60°,AB=1,E为BC的中点,则对角线BD上的动点P到E、C两点的距离之和的最小值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
分析 根据菱形的性质,得知A、C关于BD对称,根据轴对称的性质,将PM+PC转化为AP+PM,再根据两点之间线段最短得知AM为PM+PC的最小值.
解答 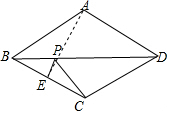 解:∵四边形ABCD为菱形,
解:∵四边形ABCD为菱形,
∴A、C关于BD对称,
∴连AE交BD于P,
则PE+PC=PE+AP=AE,
根据两点之间线段最短,AE的长即为PE+PC的最小值.
∵∠ABC=60°,
∴∠ABE=∠BAC=60°,
∴△ABC为等边三角形,
又∵BE=CE,
∴AE⊥BC,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\frac{\sqrt{3}}{2}$.
故选C.
点评 此题考查了轴对称---最短路径问题,解答过程要利用菱形的性质及等腰三角形的性质,转化为两点之间线段最短的问题来解.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
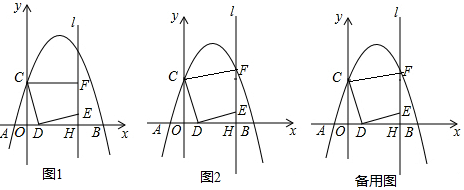
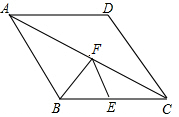 如图,点E为菱形ABCD的BC边的中点,动点F在对角线AC上运动,连接BF、EF,设AF=x,△BEF的周长为y,那么能表示y与x的函数关系的大致图象是( )
如图,点E为菱形ABCD的BC边的中点,动点F在对角线AC上运动,连接BF、EF,设AF=x,△BEF的周长为y,那么能表示y与x的函数关系的大致图象是( )| A. | 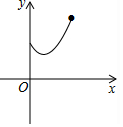 | B. | 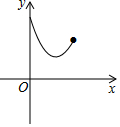 | C. | 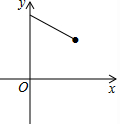 | D. | 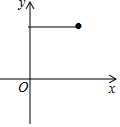 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 中位数是10 | B. | 众数是10 | C. | 平均数是9.5 | D. | 方差是16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对某区中小学生的睡眠时间的调查 | |
| B. | 对我市初中学生的兴趣爱好的调查 | |
| C. | 对我市中学教师的健康状况的调查 | |
| D. | 对“天宫二号”飞行器各零部件的质量的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com