
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数 ![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.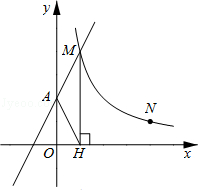
(1)求k的值;
(2)点N(a,1)是反比例函数 ![]() (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:由y=2x+2可知A(0,2),即OA=2.
∵tan∠AHO=2,∴OH=1.
∵MH⊥x轴,∴点M的横坐标为1.
∵点M在直线y=2x+2上,
∴点M的纵坐标为4.即M(1,4).
∵点M在y= ![]() 上,
上,
∴k=1×4=4
(2)
解:存在.
过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示).此时PM+PN最小.

∵点N(a,1)在反比例函数 ![]() (x>0)上,
(x>0)上,
∴a=4.即点N的坐标为(4,1).
∵N与N1关于x轴的对称,N点坐标为(4,1),
∴N1的坐标为(4,﹣1).
设直线MN1的解析式为y=kx+b.
由 ![]() 解得k=﹣
解得k=﹣ ![]() ,b=
,b= ![]() .
.
∴直线MN1的解析式为 ![]() .
.
令y=0,得x= ![]() .
.
∴P点坐标为( ![]() ,0)
,0)
【解析】(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1 , 连接MN1与x轴的交点就是满足条件的P点位置.


科目:初中数学 来源: 题型:
【题目】九年级七班“数学兴趣小组”对函数的对称变换进行探究,以下是探究发现运用过程,请补充完整.
(1)操作发现,在作函数y=|x|的图象时,采用了分段函数的办法,该函数转化为y= ![]() ,请在如图1所示的平面直角坐标系中作出函数的图象;
,请在如图1所示的平面直角坐标系中作出函数的图象;
(2)类比探究
作函数y=|x﹣1|的图象,可以转化为分段函数 , 然后分别作出两段函数的图象.聪明的小昕,利用坐标平面上的轴对称知识,把函数y=x﹣1在x轴下面部分,沿x轴进行翻折,与x轴上及上面部分组成了函数y=|x﹣1|的图象,如图所示;
(3)拓展提高
如图2右图是函数y=x2﹣2x﹣3的图象,请在原坐标系作函数y=|x2﹣2x﹣3|的图象;
(4)实际运用
①函数 ![]() 的图象与x轴有个交点,对应方程|x2﹣2x﹣3|=0有个实根;
的图象与x轴有个交点,对应方程|x2﹣2x﹣3|=0有个实根;
②函数 ![]() 的图象与直线y=5有个交点,对应方程|x2﹣2x﹣3|=5有个实根;
的图象与直线y=5有个交点,对应方程|x2﹣2x﹣3|=5有个实根;
③函数 ![]() 的图象与直线y=4有个交点,对应方程
的图象与直线y=4有个交点,对应方程 ![]() 有个实根;
有个实根;
④关于x的方程 ![]() 有4个实根时,a的取值范围是 .
有4个实根时,a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y= ![]() x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 . 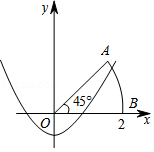
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a+b=1,ab=-1.设![]()
(1)计算S2;
(2)请阅读下面计算S3的过程: ![]()
=![]()
=![]()
=![]()
∵a+b=1,ab=-1,
∴![]() _______.
_______.
你读懂了吗?请你先填空完成(2)中S3的计算结果;再计算S4;
(3)猜想并写出![]() ,
, ![]() ,
, ![]() 三者之间的数量关系(不要求证明,且n是不小于2的自然数),根据得出的数量关系计算S3.
三者之间的数量关系(不要求证明,且n是不小于2的自然数),根据得出的数量关系计算S3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线AD、中线BE相交于点O,则①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线.4个结论中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( )
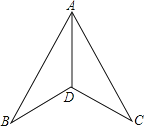
A. BD=DC,AB=AC B. ∠B=∠C,BD=DC
C. ∠B=∠C,∠BAD=∠CAD D. ∠ADB=∠ADC,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点 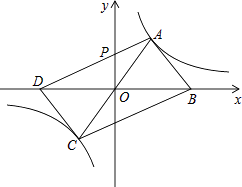
(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)在(1)的条件下,若△APO的面积为2,求点D到直线AC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2 , 以OA2为直角边作等腰Rt△OA2A3 , …则OA6的长度为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com