
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 ①由勾股定理判定;②直接利用全等三角形的判定与性质以及利用平行四边形的性质求出即可;
解答 解:①直角三角形中两条直角边的平方和等于斜边的平方,故①正确;
②一组对边相等,一组对角相等的四边形不一定是平行四边形,所以②错误;
③对角线互相垂直的平行四边形是菱形,所以③错误;
④三角形的中位线平行于三角形的第三边,且等于第三边的一半,所以④正确;
⑤对角线相等且互相平分的四边形是矩形,⑤正确;
故选B.
点评 本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题叫定理.也考查了特殊四边形的判定方法;判断命题的真假关键是要熟悉课本中的性质定理.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:初中数学 来源: 题型:填空题
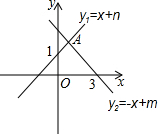 如图所示,直线y1=x+n与y轴交于点(0,1),直线y2=-x+m与x轴交于点(3,0),两直线交于点A.不等式x+n≥-x+m的解集为x≥1.
如图所示,直线y1=x+n与y轴交于点(0,1),直线y2=-x+m与x轴交于点(3,0),两直线交于点A.不等式x+n≥-x+m的解集为x≥1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
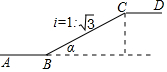 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,电梯坡面BC的坡度i=1:$\sqrt{3}$,则电梯坡面BC的坡角α为( )
如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,电梯坡面BC的坡度i=1:$\sqrt{3}$,则电梯坡面BC的坡角α为( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com