
 如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( )
如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( )| A. | $\sqrt{3}-\frac{π}{2}$ | B. | $\sqrt{3}-\frac{3}{2}π$ | C. | 2$-\frac{π}{3}$ | D. | $\sqrt{3}-\frac{π}{3}$ |
分析 由于六边形ABCDEF是正六边形,所以∠AOB=60°,故△OAB是等边三角形,OA=OB=AB=2,设点G为AB与⊙O的切点,连接OG,则OG⊥AB,OG=OA•sin60°,再根据S阴影=S△OAB-S扇形OMN,进而可得出结论.
解答  解:∵六边形ABCDEF是正六边形,
解:∵六边形ABCDEF是正六边形,
∴∠AOB=60°,
∴△OAB是等边三角形,OA=OB=AB=2,
设点G为AB与⊙O的切点,连接OG,则OG⊥AB,
∴OG=OA•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴S阴影=S△OAB-S扇形OMN=$\frac{1}{2}$×2×$\sqrt{3}$-$\frac{60π×(\sqrt{3})^{2}}{360}$=$\sqrt{3}$-$\frac{π}{2}$.
故选A.
点评 本题考查的是正多边形和圆,根据正六边形的性质求出△OAB是等边三角形是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 若实数a、b在数轴上对应点的位置如图所示,则$\sqrt{{a}^{2}-2ab+{b}^{2}}$可化简为( )
若实数a、b在数轴上对应点的位置如图所示,则$\sqrt{{a}^{2}-2ab+{b}^{2}}$可化简为( )| A. | a+b | B. | a-b | C. | b-a | D. | -a-b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
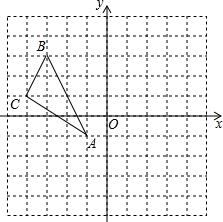 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1)
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省九年级三月月考数学试卷(解析版) 题型:判断题
如图,抛物线  交
交  轴于点
轴于点  和点
和点  ,交
,交  轴于点
轴于点  .
.
(1)求抛物线的函数表达式;
(2)若点  在抛物线上,且
在抛物线上,且  ,求点
,求点  的坐标;
的坐标;
(3)如图 b,设点  是线段
是线段  上的一动点,作
上的一动点,作  轴,交抛物线于点
轴,交抛物线于点  ,求线段
,求线段  长度的最大值.
长度的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com