
绘制函数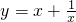 的图象,我们经历了如下过程:确定自变量x的取值范围是x≠0; 列表--描点--连线,得到该函数的图象如图所示.
的图象,我们经历了如下过程:确定自变量x的取值范围是x≠0; 列表--描点--连线,得到该函数的图象如图所示.
| x | … | -4 | -3 | -2 | -1 | - | - | - |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … | 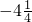 | 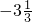 | 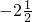 | -2 | 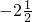 | 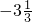 | 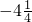 |  | 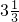 | 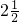 | 2 | 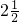 | 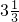 |  | … |
 观察函数图象,回答下列问题:
观察函数图象,回答下列问题:
(1)函数图象在第______象限;
(2)函数图象的对称性是______
A.既是轴对称图形,又是中心对称图形 B.只是轴对称图形,不是中心对称图形
C.不是轴对称图形,而是中心对称图形 D.既不是轴对称图形,也不是中心对称图形
(3)在x>0时,当x=______时,函数y有最______(大,小)值,且这个最值等于______;
在x<0时,当x=______时,函数y有最______(大,小)值,且这个最值等于______;
(4)方程 是否有实数解?说明理由.
是否有实数解?说明理由.

 =-2x+1没有实数解,理由为:y=x+
=-2x+1没有实数解,理由为:y=x+ 与y=-2x+1在同一直角坐标系中无交点.
与y=-2x+1在同一直角坐标系中无交点. 与y=-2x+1的交点横坐标,由图形可知两函数图象没有交点,故所求方程没有实数根.
与y=-2x+1的交点横坐标,由图形可知两函数图象没有交点,故所求方程没有实数根.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
| 1 |
| x |
| x | … | -4 | -3 | -2 | -1 | -
|
-
|
-
|
|
|
|
1 | 2 | 3 | 4 | … | ||||||||||||||||||||||||
| y | … | -4
|
-3
|
-2
|
-2 | -2
|
-3
|
-4
|
4
|
3
|
2
|
2 | 2
|
3
|
4
|
… |
 观察函数图象,回答下列问题:
观察函数图象,回答下列问题:| 1 |
| x |
查看答案和解析>>
科目:初中数学 来源:2012年江西省南昌市中考数学试卷(样卷)(解析版) 题型:解答题
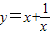 的图象,我们经历了如下过程:确定自变量x的取值范围是x≠0; 列表--描点--连线,得到该函数的图象如图所示.
的图象,我们经历了如下过程:确定自变量x的取值范围是x≠0; 列表--描点--连线,得到该函数的图象如图所示. | x | … | -4 | -3 | -2 | -1 | - | - | - |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … |  |  |  | -2 |  | 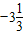 |  |  |  |  | 2 |  |  |  | … |
 是否有实数解?说明理由.
是否有实数解?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com