
【题目】过三点A(2,2),B(6,2),C(4,5)的圆的圆心坐标为_____.
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,交
,交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() .有以下结论:①
.有以下结论:①![]() 平分
平分![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④
是等边三角形;④![]() ,则正确的结论有( )
,则正确的结论有( )
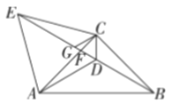
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
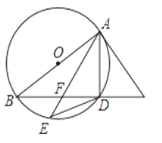
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,称“对顶三角形”,其中,∠A+∠B=∠C+∠D
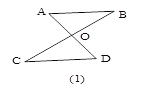

利用这个结论,完成下列填空.
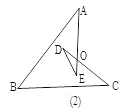
(1)如图 (2),∠A+∠B+∠C+∠D+∠E= ;
(2)如图(3),∠A+∠B+∠C+∠D+∠E= ;
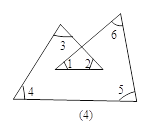
(3)如图(4),∠1+∠2+∠3+∠4+∠5+∠6= ;
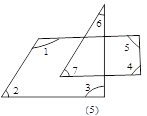
(4)如图(5),∠1+∠2+∠3+∠4+∠5+∠6+∠7= .
查看答案和解析>>
科目:初中数学 来源: 题型:
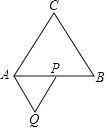
【题目】如图,等边△ABC的边长为6,点P沿△ABC的边从A→B→C运动,以AP为边作等边△APQ,且点Q在直线AB下方,当点P、Q运动到使△BPQ是等腰三角形时,点Q运动路线的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在⊙O的直径AB的延长线上,PC为⊙O的切线,点C为切点,连接AC,过点A作PC的垂线,点D为垂足,AD交⊙O于点E.
(1)如图1,求证:∠DAC=∠PAC;
(2)如图2,点F(与点C位于直径AB两侧)在⊙O上,![]() ,连接EF,过点F作AD的平行线交PC于点G,求证:FG=DE+DG;
,连接EF,过点F作AD的平行线交PC于点G,求证:FG=DE+DG;
(3)在(2)的条件下,如图3,若AE=![]() DG,PO=5,求EF的长.
DG,PO=5,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
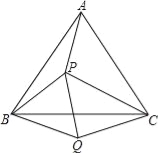
【题目】如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论错误的是( )
A.△BPQ是等边三角形
B.△PCQ是直角三角形
C.∠APB=150°
D.∠APC=135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系网格中,格点A的位置如图所示:

(1)若点B坐标为(2,3),请你画出△AOB;
(2)若△AOB与△A′O′B′关于y轴对称,请你画出△A′O′B';
(3)请直接写出线段AB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com