
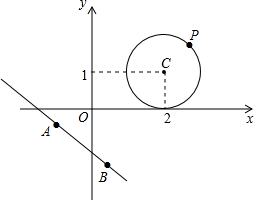
 �Ķ����ϣ�
�Ķ����ϣ����� ��1�����ݵ㵽ֱ�ߵľ��빫ʽ���Ǽ��ɣ�
��2�����ݵ㵽ֱ�ߵľ��빫ʽ���г����̼��ɽ�����⣮
��3�����Բ��C��ֱ��3x+4y+5=0�ľ��룬�����C�ϵ�P��ֱ��3x+4y+5=0�ľ�������ֵ�Լ���Сֵ���ɽ�����⣮
��� �⣺��1����P1��3��4����ֱ��3x+4y-5=0�ľ���d=$\frac{|3��3+4��4-5|}{\sqrt{{3}^{2}+{4}^{2}}}$=4��
�ʴ�Ϊ4��
��2���ߡ�C��ֱ��y=-$\frac{3}{4}$x+b���У���C�İ뾶Ϊ1��
��C��2��1����ֱ��3x+4y-4b=0�ľ���d=1��
��$\frac{|6+4-4b|}{\sqrt{{3}^{2}+{4}^{2}}}$=1��
���b=$\frac{5}{4}$��$\frac{15}{4}$��
��3����C��2��1����ֱ��3x+4y+5=0�ľ���d=$\frac{|6+4+5|}{\sqrt{{3}^{2}+{4}^{2}}}$=3��
���C�ϵ�P��ֱ��3x+4y+5=0�ľ�������ֵΪ4����СֵΪ2��
��S��ABP�����ֵ=$\frac{1}{2}$��2��4=4��S��ABP����Сֵ=$\frac{1}{2}$��2��2=2��
���� ���⿼��һ�κ����ۺ��⣬�㵽ֱ�ߵľ��빫ʽ��ֱ����Բ��λ�ù�ϵ��֪ʶ������Ĺؼ����������⣬ѧ���ֱ�ߵĽ���ʽת��ΪAx+By+C=0����ʽ��ѧ�ṹ�����̽�����⣬����Բ�ϵĵ㵽ֱ�ߵľ�������ֵ�Լ���Сֵ�������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
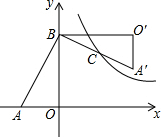 ��ͼ����Rt��AOB�У���ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�����AOB�Ƶ�B��ʱ����ת90���õ���A��O��B��������������y=$\frac{k}{x}$��ͼ��ǡ�þ���б��A��B���е�C��S��ABO=16��tan��BAO=2����k��ֵΪ��������
��ͼ����Rt��AOB�У���ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�����AOB�Ƶ�B��ʱ����ת90���õ���A��O��B��������������y=$\frac{k}{x}$��ͼ��ǡ�þ���б��A��B���е�C��S��ABO=16��tan��BAO=2����k��ֵΪ��������| A�� | 20 | B�� | 22 | C�� | 24 | D�� | 26 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
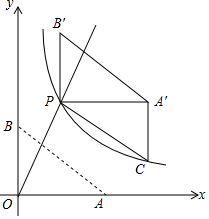 ��ͼ��ֱ��y=k1x��x��0����˫����y=$\frac{k_2}{x}$��x��0���ཻ�ڵ�P��2��4������֪��A��4��0����B��0��3��������AB����Rt��AOB��OP����ƽ�ƣ�ʹ��O�ƶ�����P���õ���A'PB'������A'��A'C��y�ύ˫�����ڵ�C��
��ͼ��ֱ��y=k1x��x��0����˫����y=$\frac{k_2}{x}$��x��0���ཻ�ڵ�P��2��4������֪��A��4��0����B��0��3��������AB����Rt��AOB��OP����ƽ�ƣ�ʹ��O�ƶ�����P���õ���A'PB'������A'��A'C��y�ύ˫�����ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4��5֮�� | B�� | 5��6֮�� | C�� | 6��7֮�� | D�� | 7��8֮�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ���ɰ����ҹ����ȵ�һ��Խ���죮�����ķ�ͼ����������С������ͼ��ʾ�����ɰ�ƴ�ɵģ�����С��ƴ�ɵ��Ǹ�ͼ�ǣ�������
���ɰ����ҹ����ȵ�һ��Խ���죮�����ķ�ͼ����������С������ͼ��ʾ�����ɰ�ƴ�ɵģ�����С��ƴ�ɵ��Ǹ�ͼ�ǣ�������| A�� | 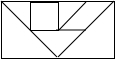 | B�� |  | ||
| C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
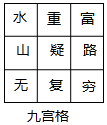 Ϊ�˱���������㴫ͳ�Ļ���ijУ��֯��һ�Ρ�ʫ�ʴ�ᡱ��С����С��ͬʱ�μӣ����У���һ���ش����ǣ�����ͼ��ʾ�ľŹ�����ѡȡ�߸������һ����ʫ�����Ϊ��ɽ��ˮ������·����
Ϊ�˱���������㴫ͳ�Ļ���ijУ��֯��һ�Ρ�ʫ�ʴ�ᡱ��С����С��ͬʱ�μӣ����У���һ���ش����ǣ�����ͼ��ʾ�ľŹ�����ѡȡ�߸������һ����ʫ�����Ϊ��ɽ��ˮ������·�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
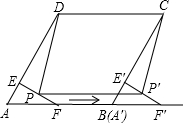 ��ͼ��������ABCD�У���A=60�㣬AD=8��F��AB���е㣮����F��FE��AD������ΪE������AEF�ص�A����B�ķ���ƽ�ƣ��õ���A'E'F'���� P��P'�ֱ��� EF��E'F'���е㣬����A'���B�غ�ʱ���ı���PP'CD�����Ϊ��������
��ͼ��������ABCD�У���A=60�㣬AD=8��F��AB���е㣮����F��FE��AD������ΪE������AEF�ص�A����B�ķ���ƽ�ƣ��õ���A'E'F'���� P��P'�ֱ��� EF��E'F'���е㣬����A'���B�غ�ʱ���ı���PP'CD�����Ϊ��������| A�� | 28$\sqrt{3}$ | B�� | 24$\sqrt{3}$ | C�� | 32$\sqrt{3}$ | D�� | 32$\sqrt{3}$-8 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com