

| A.3cm | B.4cm | C.5cm | D.4.5cm |
 =6cm,
=6cm,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
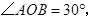 过
过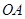 上到点
上到点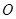 的距离为1,3,5,7,…的点作
的距离为1,3,5,7,…的点作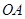 的垂线,分别与
的垂线,分别与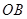 相交,得到图所示的阴影梯形,它们的面积依次记为
相交,得到图所示的阴影梯形,它们的面积依次记为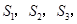 ….则
….则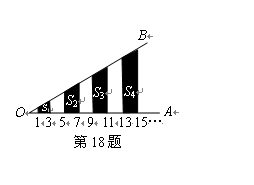
 ;
;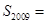 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (四个角都是直角,四边都相等,边长
(四个角都是直角,四边都相等,边长 的余料,修剪成如四边形
的余料,修剪成如四边形 的零件. 其中
的零件. 其中 ,
, 是
是 的中点.
的中点.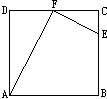
 的代数式表示
的代数式表示 的值;
的值; ,则△
,则△ 是直角三角形吗?为什么?
是直角三角形吗?为什么?查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y >0),当x = ,公共部分面积y最大,y最大值 = ,
两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y >0),当x = ,公共部分面积y最大,y最大值 = ,
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.20° |
| B.30° |
| C.45° |
| D.60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com