
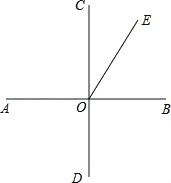
【题目】如图,AB垂直CD(即∠AOC=∠AOD=∠BOD=∠BOC=90°)
(1)比较∠AOD,∠EOB,∠AOE大小(用“<”连接)
(2)如∠EOC=28°,求∠EOB和∠EOD的度数(适当写出解题过程)
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )

A.(﹣3,0) B.(﹣6,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习过程中遇到这样一个问题:
“一个木箱漂浮在河水中,随河水向下游漂去,在木箱上游和木箱下游各有一条小船,分别为甲船和乙船,两船距木箱距离相等,同时划向木箱,若两船在静水中划行的速度是30m/min,那么哪条小船先遇到木箱?”
小明是这样分析解决的:
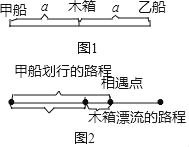
小明想通过比较甲乙两船遇见木箱的时间,知道哪条小船先遇见木箱.设甲船遇见木箱的时间为xmin,乙船遇见木箱的时间为ymin,开始时两船与木箱距离相等,都设为am,如图1.
如图2,利用甲船划行的路程﹣木箱漂流的路程=开始时甲船与木箱的距离:
列方程:x(30+5)﹣5x=a
解得,x=![]()
所以甲船遇见木箱的时间为![]() min.
min.
(1)参照小明的解题思路继续完成上述问题;
(2)借鉴小明解决问题的方法和(1)中发现的结论解决下面问题:
问题:“在一河流中甲乙两条小船,同时从A地出发,甲船逆流而上,乙船顺流而下;划行10分钟后,乙船发现船上木箱不知何时掉入水中,乙船立即通知甲船,两船同时掉头寻找木箱,若两船在静水中划行的速度是v(单位:m/min,v大于5),水流速度是5m/min,两船同时遇见木箱,那么木箱是出发几分钟后掉入水中的?”
查看答案和解析>>
科目:初中数学 来源: 题型:
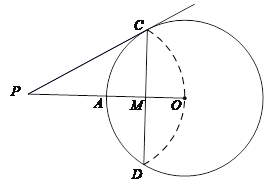
【题目】如图,已知⊙O的半径为4,OA为半径,CD为弦,OA与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.
(1)求CD的长;
(2)求证:PC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四个完全相同的小球上分别写有:0, ![]() ,﹣5,π四个实数,把它们全部装入一个布袋里,从布袋里任意摸出1个球,球上的数是无理数的概率为 .
,﹣5,π四个实数,把它们全部装入一个布袋里,从布袋里任意摸出1个球,球上的数是无理数的概率为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设A:踢毽子;B:篮球:C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如两个统计图.请结合图中的信息解答下列问题:
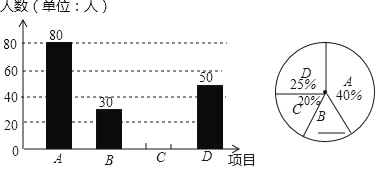
(1)本次共调查了多少名学生?
(2)请将两个统计图补充完整.
(3)求图中“A”层次所在扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天的早晨,小明骑自行车从家出发,到离家1050米的书店买书,出发1分钟后,他到达离家150米的地方,又过1分钟后,小明加快了速度.如图所示是小明从家出发后离家的路程y(米)与他骑自行车的时间x(分钟)之间的函数图象.根据图象解答下列问题: 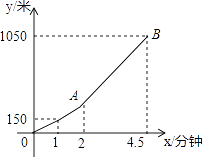
(1)直接写出点A的坐标,并求线段AB所在的直线的函数解析式.
(2)求小明出发多长时间后,离书店还剩210米的路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com