
已知图中的曲线是函数 (m为常数)图象的一支.
(m为常数)图象的一支.
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数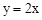 图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
(1)m>5;(2)点A的坐标为(2,4);反比例函数的解析式为 .
.
解析试题分析:(1)曲线函数 (m为常数)图象的一支在第一象限,则比例系数m-5一定大于0,即可求得m的范围;
(m为常数)图象的一支在第一象限,则比例系数m-5一定大于0,即可求得m的范围;
(2)把A的坐标代入正比例函数解析式,即可求得A的坐标,再代入反比例函数解析式即可求得反比例函数解析式.
试题解析:(1)∵函数 (m为常数)图象的一支在第一象限,∴m-5>0,解得m>5.
(m为常数)图象的一支在第一象限,∴m-5>0,解得m>5.
(2)∵函数 的图象与正比例函数
的图象与正比例函数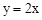 的图象在第一象限的交点为A(2,n),
的图象在第一象限的交点为A(2,n),
∴ ,解得
,解得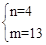 .
.
∴点A的坐标为(2,4);反比例函数的解析式为 .
.
考点:1.反比例函数和正比例函数的图象交点问题;2.曲线上点的坐标与方程的关系;3.反比例函数的性质.


科目:初中数学 来源: 题型:填空题
如图,在平面直角坐标系 中,已知直线l:
中,已知直线l: ,双曲线
,双曲线 。在l上取点A1,过点A1作
。在l上取点A1,过点A1作 轴的垂线交双曲线于点B1,过点B1作
轴的垂线交双曲线于点B1,过点B1作 轴的垂线交于点A2,请继续操作并探究:过点A2作
轴的垂线交于点A2,请继续操作并探究:过点A2作 轴的垂线交双曲线于点B2,过点B2作
轴的垂线交双曲线于点B2,过点B2作 轴的垂线交于点A3,…,这样依次得到上的点A1,A2,A3,…,An,…。记点An的横坐标为
轴的垂线交于点A3,…,这样依次得到上的点A1,A2,A3,…,An,…。记点An的横坐标为 ,若
,若 ,则
,则 = ,
= , = ;若要将上述操作无限次地进行下去,则
= ;若要将上述操作无限次地进行下去,则 不能取的值是__________
不能取的值是__________
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某乡要在生活垃圾存放区建一个老年活动中心,这样必须把1 200 m3的生活垃圾运走.
(1)假如每天能运x m3,所需时间为y天,写出y与x之间的函数关系式;
(2)若每辆拖拉机一天能运12 m3,则5辆这样的拖拉机要多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,O为坐标原点,P是反比例函数 (x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(1)求证:线段AB为⊙P的直径;
(2)求△AOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图, .
. 是反比例函数
是反比例函数 (k>0)在第一象限图象上的两点,点
(k>0)在第一象限图象上的两点,点 的坐标为(2,0),若△
的坐标为(2,0),若△ 与△
与△ 均为等边三角形.
均为等边三角形.
(1)求此反比例函数的解析式;
(2)求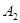 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,反比例函数 的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
(1)求一次函数的表达式;
(2)观察图象,直接写出使反比例函数值大于一次函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图在平面直角坐标系xOy中,函数 (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数y=2x﹣2的图象与x轴、y轴分别相交于B、A两点,与反比例函数 的图象在第一象限内的交点为M(3,m).
的图象在第一象限内的交点为M(3,m).
(1)求反比例函数的解析式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com