
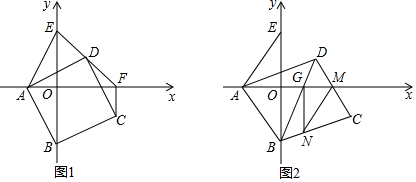
分析 (1)取OF的中点为H,连接DH,则可证得△AHD≌△EOA,则可求得AO和OE的长,即可求得A、E的坐标,利用待定系数法可求得直线AE解析式;
(2)连接OD,可证明△ODA≌△FDC,则可得FC=OA,可求得FC的长;
(3)作GK⊥AB于K,GQ⊥BC于Q,可证明△AKG≌△GQN,延长NB到P使BP=DM,可证明△ABP≌△ADM,进一步可证△PAN≌△MAN,利用全等三角形的性质,可得出结论.
解答 解:
(1)如图1,取OF的中点H,连DH,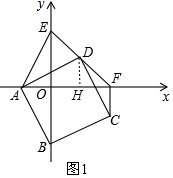
则DH为△EOF的中位线,
∴DH=OH=HF,
∵四边形ABCD为正方形,
∴∠BAD=90°,AD=BC,
∴∠BAO+∠DAH=∠ABO+∠BAO=90°,
∴∠ABO=∠DAO,
∵B、E关于x轴对称,
∴∠ABO=∠AEO,AB=AE,
∴∠AEO=∠DAH,AD=AE,
在△AHD和△EOA中
$\left\{\begin{array}{l}{∠AHD=∠AOE}\\{∠DAH=∠AEO}\\{AD=AE}\end{array}\right.$
∴△AHD≌△EOA(AAS),
∴OA=DH=HF=OH,OE=AH,
∴OE=2AO,
∵AE=10,
∴AO=$2\sqrt{5}$,OE=$4\sqrt{5}$,
即A(-$2\sqrt{5}$,0),E(0,$4\sqrt{5}$),
∴可设直线AE解析式为y=kx+4$\sqrt{5}$,
∴-2$\sqrt{5}$k+4$\sqrt{5}$=0,解得k=2,
∴直线AE的解析式为$y=2x+4\sqrt{5}$;
(2)如图2,连接OD,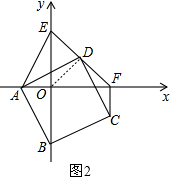
∵∠ODF=∠ADC=90°,
∴∠ODA=∠FDC,
在△ODA和△FDC中
$\left\{\begin{array}{l}{OD=DF}\\{∠ODA=∠FDC}\\{AD=CD}\end{array}\right.$
∴△ODA≌△FDC(SAS),
∴FC=OA=$2\sqrt{5}$;
(3)如图3,作GK⊥AB于K,GQ⊥BC于Q,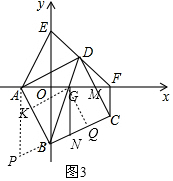
∵点G在正方形ABCD的对角线上,
∴GK=GQ,
∵∠AGK+∠KGN=∠KGN+∠NGQ=90°,
∴∠AGK=∠NGQ,
在△AKG和△GQN中
$\left\{\begin{array}{l}{∠AKG=∠GQN}\\{KG=QG}\\{∠AGK=∠NGQ}\end{array}\right.$
∴△AKG≌△GQN(ASA),
∴AG=GN,
∴∠GAN=45°,
延长NB到P使BP=DM,
在△ABP和△ADM中
$\left\{\begin{array}{l}{AB=AD}\\{∠ABP=∠ADM}\\{BP=DM}\end{array}\right.$
∴△ABP≌△ADM(SAS),
∴AM=AP,∠PAB=∠MAD,
∴∠PAN=∠PAB+∠BAN=∠MAD+∠BAN=∠GAN=45°,
∴△PAN≌△MAN,
∴MN=PN=BN+DM.
点评 本题为一次函数的综合应用,涉及待定系数法、正方形的性质、全等三角形的判定和性质等知识.在(1)中求得A、E的坐标是解题的关键,在(2)中证得△ODA≌△FDC是解题的关键,在(3)中构造三角形全等是解题的关键.本题考查知识点较多,综合性较强,难度较大.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
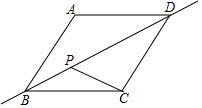 如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+$\frac{PB}{2}$的值最小时,线段PD的长是( )
如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+$\frac{PB}{2}$的值最小时,线段PD的长是( )| A. | $\frac{4}{3}\sqrt{3}$ | B. | $\frac{2}{3}\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{4}{3}\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
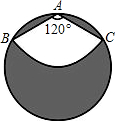 如图所示,有一个直径是1m的圆形铁皮,要从中剪出一个半径为$\frac{1}{2}$且圆心角是120°的扇形ABC.求被剪掉后剩余阴影部分的面积.
如图所示,有一个直径是1m的圆形铁皮,要从中剪出一个半径为$\frac{1}{2}$且圆心角是120°的扇形ABC.求被剪掉后剩余阴影部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
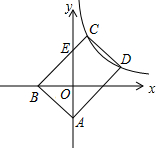 如图,平行四边形ABCD中A点的坐标为(0,-2),B在x轴的负半轴上,C、D两点落在反比例函数y=kx-1上,且D点的横坐标为3,四边形AECD的面积是三角形ABE面积的3倍.求k的值.
如图,平行四边形ABCD中A点的坐标为(0,-2),B在x轴的负半轴上,C、D两点落在反比例函数y=kx-1上,且D点的横坐标为3,四边形AECD的面积是三角形ABE面积的3倍.求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2种 | B. | 3种 | C. | 4种 | D. | 5种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com