
【题目】如图①,在平行四边形ABCD中,对角线AC、BD交于点O,AB=AC,AB⊥AC,过点A作AE⊥BD于点E.
(1)若BC=6![]() ,求AE的长度;
,求AE的长度;
(2)如图②,点F是BD上一点,连接AF,过点A作AG⊥AF,且AG=AF,连接GC交AE于点H,证明:GH=CH.

【答案】(1)AE=![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据题意可得:AB=AC=6,可得AO=3,根据勾股定理可求BO的值,根据S△ABO=![]() AB×BO=
AB×BO=![]() BO×AE,可求AE的长度.
BO×AE,可求AE的长度.
(2)延长AE到P,使AP=BF,可证△ABF≌△APC,可得AF=PC.则GA=PC,由AG⊥AF,AE⊥BE可得∠GAH=∠BFA=∠APC,可证△AGH≌△PHC,结论可得.
解:(1)∵AB=AC,AB⊥AC,BC=6![]()
∴AB2+AC2=BC2,
∴2AC2=72
∴AC=AB=6
∵四边形ABCD是平行四边形
∴AO=CO=3
在Rt△AOB中,BO=![]() =3
=3![]()
∵S△ABO=![]() AB×BO=
AB×BO=![]() BO×AE
BO×AE
∴3×6=3![]() ×AE
×AE
∴AE=![]()
(2)如图:延长AE到P,使AP=BF
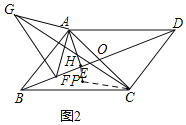
∵∠BAC=90°,AE⊥BE
∴∠BAE+∠ABE=90°,∠BAE+∠CAE=90°
∴∠ABE=∠CAE且AB=AC,BF=AP
∴△ABF≌△APC
∴AF=PC,∠AFB=∠APC
∵AG⊥AF,AG=AF
∴AG=PC
∵∠GAH=∠GAF+∠FAE=90°+∠FAE,∠AFB=∠AEB+∠FAE=90°+∠FAE
∴∠GAH=∠AFB
∴∠AFB=∠GAH=∠APC,且AG=PC,∠GHA=∠CHP
∴△AGH≌△CHP
∴GH=HC


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,三角形![]() 是以
是以![]() 为底边的等腰三角形,点
为底边的等腰三角形,点![]() 、
、![]() 分别是一次函数
分别是一次函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴的交点,点
轴的交点,点![]() 在二次函数
在二次函数![]() 的图象上,且该二次函数图象上存在一点
的图象上,且该二次函数图象上存在一点![]() 使四边形
使四边形![]() 能构成平行四边形.
能构成平行四边形.

(1)试求![]() 、
、![]() 的值,并写出该二次函数表达式;
的值,并写出该二次函数表达式;
(2)动点![]() 沿线段
沿线段![]() 从
从![]() 到
到![]() ,同时动点
,同时动点![]() 沿线段
沿线段![]() 从
从![]() 到
到![]() 都以每秒1个单位的速度运动,问:
都以每秒1个单位的速度运动,问:
①当![]() 运动过程中能否存在
运动过程中能否存在![]() ?如果不存在请说明理由;如果存在请说明点的位置?
?如果不存在请说明理由;如果存在请说明点的位置?
②当![]() 运动到何处时,四边形
运动到何处时,四边形![]() 的面积最小?此时四边形
的面积最小?此时四边形![]() 的面积是多少?
的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】单靠“死”记还不行,还得“活”用,姑且称之为“先死后活”吧。让学生把一周看到或听到的新鲜事记下来,摒弃那些假话套话空话,写出自己的真情实感,篇幅可长可短,并要求运用积累的成语、名言警句等,定期检查点评,选择优秀篇目在班里朗读或展出。这样,即巩固了所学的材料,又锻炼了学生的写作能力,同时还培养了学生的观察能力、思维能力等等,达到“一石多鸟”的效果。 如图,由两个相同的正方体和一个圆锥体组成一个立体图形,其左视图是( )

A. B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )

A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
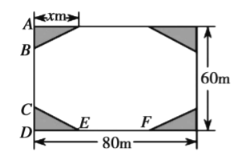
【题目】应我市创建文明城市要求,某小区业主委员会决定把一块长![]() ,宽
,宽![]() 的矩形空地建成,花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度-样,其宽度不小于
的矩形空地建成,花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度-样,其宽度不小于![]() ,不大于
,不大于![]() ,预计活动区造价
,预计活动区造价![]() ,绿化区造价
,绿化区造价![]() ,设绿化区较长直角边为
,设绿化区较长直角边为![]() .
.
(1)求工程队总造价![]() (元)与
(元)与![]() 的函数关系式,并求出x的取值范围;
的函数关系式,并求出x的取值范围;
(2)如果业主委员会最多投资![]() 万元,能否完成全部工程?若能,请写出
万元,能否完成全部工程?若能,请写出![]() 为整数的所有工程方案;若不能,请说明理由.
为整数的所有工程方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校决定从甲、乙两名同学中选拔一人参加“诵读经典”大赛,在相同的测试条件下,甲、乙两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83.
乙:88,81,85,81,80.
请回答下列问题:
(1)甲成绩的中位数是______,乙成绩的众数是______;
(2)经计算知![]() ,
,![]() .请你求出甲的方差,并从平均数和方差的角度推荐参加比赛的合适人选.
.请你求出甲的方差,并从平均数和方差的角度推荐参加比赛的合适人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
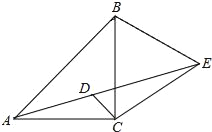
【题目】如图,等腰直角△ABC中,CA=CB,点E为△ABC外一点,CE=CA,且CD平分∠ACB交AE于D,且∠CDE=60°.
(1)求证:△CBE为等边三角形;
(2)若AD=5,DE=7,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取一点O,以点O为圆心,OF为半径作⊙O与AD相切于点P.AB=6,BC=![]()
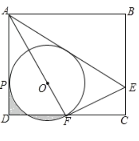
(1)求证:F是DC的中点.
(2)求证:AE=4CE.
(3)求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com