
【题目】在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.
已知:在![]() 中,
中,![]() 分别是边
分别是边![]() 的中点.
的中点.
求证: .
证明:如图,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,
,
···
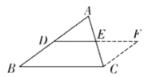
(1)补全求证:
(2)请根据添加的辅助线,写出完整的证明过程;
(3)若![]() 求边
求边![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,且
,且![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)根据需要证明的定理:三角形的中位线平行于第三边,且等于第三边的一半,即可写出答案;
(2)根据已知以及添加的辅助线,可证得△ADE![]() △CFE,进而可证明四边形BDFC是平行四边形,又因为DE=FE,即可证明结论;
△CFE,进而可证明四边形BDFC是平行四边形,又因为DE=FE,即可证明结论;
(3)在△ABC中,利用两边之和大于第三边,两边之差小于第三边,即可求解.
(1)根据题意,求证为:DE//BC,且DE=![]() BC,
BC,
(2)点E是AC的中点,
∴AE=CE,
又∵EF=ED,∠AED=∠CEF,
∴△ADE![]() △CFE,
△CFE,
∴AD=CF,∠A=∠ECF,
∴AD//CF,
∴AB//CF,
∵点D是AB的中点,
∴AD=BD,
∴BD=CF,
∴四边形BDFC是平行四边形,
∴DE//BC,DF=BC,
∵DE=FE,
∴DE=![]() BC.
BC.
(3)∵DF=8,
∴BC=8,
∵CE=3,
∴AC=6,
∴BC-AC![]() AB
AB![]() BC+AC,即2
BC+AC,即2![]() AB
AB![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将![]() 放在每个小正方形的边长为1的网格中,点
放在每个小正方形的边长为1的网格中,点![]() ,点
,点![]() ,点
,点![]() 均落在格点上.
均落在格点上.
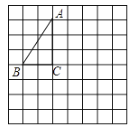
(1)![]() _________.
_________.
(2)请在如图所示的网格中,用无刻度的直尺,画出一个以![]() 为底边的等腰
为底边的等腰![]() ,使该三角形的面积等于
,使该三角形的面积等于![]() 的面积,并简要说明点
的面积,并简要说明点![]() 的位置是如何找到的(不要求证明)__________.
的位置是如何找到的(不要求证明)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 点
点![]() 在边
在边![]() 上,
上,![]() 点
点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_________ .
的长为_________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
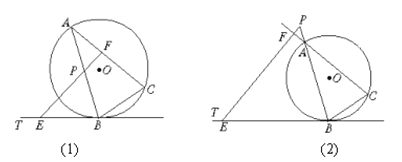
【题目】已知:△ABC是⊙O的内接三角形,BT为⊙O的切线,B为切点,P为直线AB上一点,过P作BC的平行线交直线BT于点E,交直线AC于点F.
(1)如图 (1)所示,当P在线段AB上时,求证:PA·PB=PE·PF;
(2)如图 (2)所示,当P为线段BA延长线上一点时,第(1)题的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了宣传一种新产品,在某地先后举行![]() 场产品促销会,已知该产品每台成本为
场产品促销会,已知该产品每台成本为![]() 万元,设第
万元,设第![]() 场产品的销售量为
场产品的销售量为![]() (台),在销售过程中获得以下信息:
(台),在销售过程中获得以下信息:
信息1:已知第一场销售产品![]() 台,然后每增加一场,产品就少卖出
台,然后每增加一场,产品就少卖出![]() 台;
台;
信息2:产品的每场销售单价![]() (万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次
(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次![]() 成正比,第21场--第40场浮动价与销售场次
成正比,第21场--第40场浮动价与销售场次![]() 成反比,经过统计,得到如下数据:
成反比,经过统计,得到如下数据:
| 3 | 10 | 25 |
| 10.6 | 12 | 14.2 |
(1)求![]() 与
与![]() 之间满足的函数关系式;
之间满足的函数关系式;
(2)当产品销售单价为13万元时,求销售场次是第几场?
(3)在这![]() 场产品促销会中,哪一场获得的利润最大,最大利润是多少?
场产品促销会中,哪一场获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店经销进价分别为![]() 元/千克、
元/千克、![]() 元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
时间 | 甲水果销量 | 乙水果销量 | 销售收入 |
周五 |
|
|
|
周六 |
|
|
|
(1)求甲、乙两种水果的销售单价;
(2)若水果店准备用不多于![]() 元的资金再购进两种水果共
元的资金再购进两种水果共![]() 千克,求最多能够进甲水果多少千克?
千克,求最多能够进甲水果多少千克?
(3)在(2)的条件下,水果店销售完这![]() 千克水果能否实现利润为
千克水果能否实现利润为![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
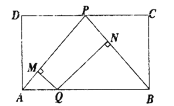
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 上的动点(不与
上的动点(不与![]() 重合).过
重合).过![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .设
.设![]() 的长度为
的长度为![]() ,
,![]() 与
与![]() 的长度和为
的长度和为![]() .则能表示
.则能表示![]() 与
与![]() 之间的函数关系的图象大致是( )
之间的函数关系的图象大致是( )
A.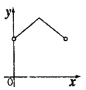 B.
B.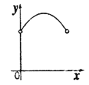 C.
C.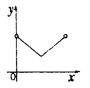 D.
D.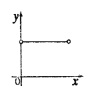
查看答案和解析>>
科目:初中数学 来源: 题型:
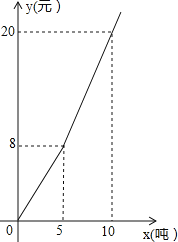
【题目】浙江实施“五水共治“以来,越来越重视节约用水,某地对居民用水按阶梯水价方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元),请根据图象信息,回答下列问题.
(1)请写出y与x的函数关系式;
(2)若某个家庭有5人,响应节水号召,计划控制1月份的生活用水费不超过76元,则该家庭这个月最多可以用多少吨水?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com